反応ギブズエネルギー\(\Delta \mathrm r G\)を、化学反応が起きた時のギブズエネルギー変化だと思っている方、それ、間違っていますよ!
本記事では、反応ギブズエネルギーとは何なのか、平衡定数との関係性、そしてそれに関連した勘違いについて解説します。
反応ギブズエネルギーに関する致命的な勘違い
学部1年生で習う基礎的な化学や、(おそらく)2年生での物理化学の授業で、教科書の後ろにある標準生成ギブズエネルギーに化学両論係数をかけて足し合わせた値を計算したことはありませんか?
あの値は標準反応ギブズエネルギーと呼ばれていますが、標準反応ギブズエネルギーの正負で反応が自発的に進むか否かがわかると思っている方、いませんか?
それ、間違っています!
標準反応ギブズエネルギーは、ギブズエネルギー自体ではありません。一体、何を意味する値なのでしょうか。
基礎: 反応進行度とは
反応進行度とは、反応がどれだけ進行したかを表す指標で、通常\(\xi\)で表記します。
反応の進行具合を表す指標を作ってみましょう。何が指標になり得るでしょうか。一番わかりやすそうなのは、反応物が減った量、あるいは生成物が増えた量でしょう。
A→Bのような反応なら、反応物が減った量と生成物が増えた量は同じなので、深いことを考えずに反応の進行具合を検討できます。
しかし、反応物が二つ以上あり、かつ化学反応式において化学両論係数が異なる場合、各反応物の減った量は互いに異なります。生成物についても同様です。そのため、化学反応式に依らない指標があれば便利です。
いま、次のような反応を考えます。
\[\mathrm{
aA+bB \to cC+dD
}\]
また、反応前と反応後における化学種\(I\)の物質量をそれぞれ\(n_{i0}\)、\(n_i\)とします。
このとき、化学種\(I\)の減少量(負の値)または増加量(正の値)は\(n_i-n_{i0}\)となります。
次に、この値を化学反応式に依らないものに調整しましょう。
化学種AとBの減少量は化学両論係数を用いて\(a:b\)になっているはずです。そのため、減少量を化学両論係数で割れば、化学反応式に依らない指標ができます。
生成物も同様に考えると、次式が成り立ちます。
\[
\frac{n_a-n_{a0}}{-a}=\frac{n_b-n_{b0}}{-b}=\frac{n_c-n_{c0}}{c}=\frac{n_d-n_{d0}}{d}
\]
これを反応進行度と呼び、\(\xi\)(ギリシャ文字のグザイ)で表記します。
\(n_i\)を化学種\(I\)の反応後における濃度、\(n_{i0}\)を化学種\(I\)の初期濃度、\(\nu_i\)を化学両論係数とすると、反応進行度\(\xi\)は次のように定義される。
\[
\xi = \frac{n_i-n_{i0}}{\nu_i}
\]
反応進行度は常に0か正の値であることをおさえておきましょう。
反応物に着目して反応進行度を計算した場合、分母と分子が共に負の値になるので、反応進行度は正になります。
一方、生成物に着目して反応進行度を反応進行度を計算すると、分母と分子が共に正になります。
また、全く反応が進んでいない場合、反応進行度は0になります。
反応ギブズエネルギーの意味
\(n_i\)を\(\xi\)で微分すると、
\[
\mathrm{d}n_i= \nu_i \mathrm{d}\xi
\tag1
\]
よって、温度と圧力を一定としたとき、ギブズエネルギーの全微分と(1)式より、
\[
\mathrm dG = \sum_{i}\mu_i \mathrm dn_i = \sum_{i}\mu_i \nu_i \mathrm d\xi
\tag2
\]
したがって、
\[
\left(
\frac
{\mathrm dG}{\mathrm d\xi}
\right)_{P,T}
=\sum_{i}\nu_i \mu_i \\
\tag3
\]
ここで、反応ギブズエネルギー\(\Delta_\mathrm rG \)を次のように定義します。
反応ギブズエネルギー\(\Delta_\mathrm rG \)を次のように定義する。
\[
\Delta_\mathrm rG :=\sum_{i}\nu_i \mu_i
\tag4
\]
すなわち、(3)式と(4)式より次式が成り立ちます。
\[\left(
\frac
{\mathrm dG}{\mathrm d\xi}
\right)_{P,T}
=\Delta_\mathrm rG
\tag5
\]
また、化学ポテンシャルのていぎから、次式が成り立ちます。
\[\begin{align}
\Delta_\mathrm rG &=\sum_{i}\nu_i \mu_i \\
&=\sum_i \nu_i({\mu_i}^\circ + RT \ln{a_i}) \\
&=\Delta_\mathrm rG^\circ
+ RT \ln
{
\prod_i {a_i}^{\nu_i}
}
\tag6
\end{align}\]
ここで、反応商\(Q\)を次のように定義します。
\[
Q:=\prod_i {a_i}^{\nu_i}
\tag7
\]
(6)と(7)より、次式が成り立ちます。
\[
\begin{align}
\left(
\frac
{\mathrm dG}{\mathrm d\xi}
\right)_{P,T}
&=\Delta_\mathrm rG \\
&=\Delta_\mathrm rG^\circ + RT \ln Q
\end{align}
\tag8
\]
つまり、標準反応ギブズエネルギーは、ギブズエネルギーを反応進行度で微分した時ときに出てくる定数項で、ギブズエネルギー自体ではありません。
反応の進行に伴うギブズエネルギー変化
大切なのは、標準反応ギブズエネルギーの項以外にも反応商の項がギブズエネルギー変化に関わっているということです。標準反応ギブズエネルギーだけで自発変化については言及できないのです。
さて、反応が進行するほど反応商の分母は小さくなり、分子は大きくなるため、(8)より、ギブズエネルギーは\(\xi\)に対して単調増加なことがわかります。
つまり横軸に反応進行度\(\xi\)、縦軸にギブズエネルギー\(G\)をとると、次のようになります。
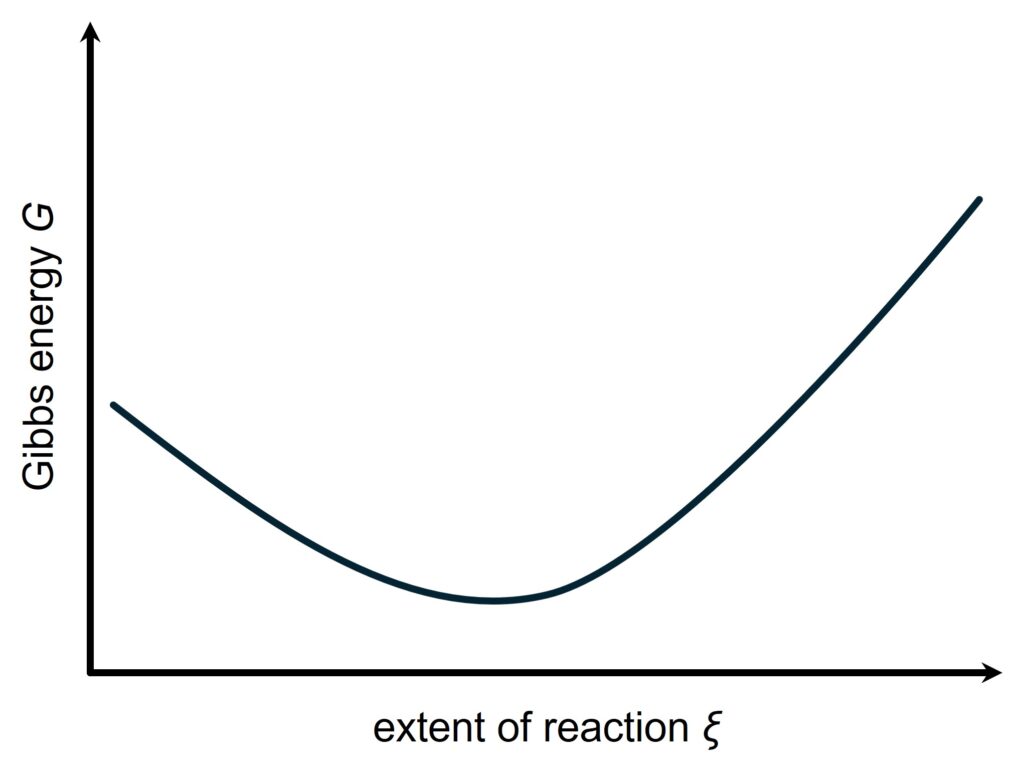
図1からわかるように、極小値は一つしかないため、平衡になる反応進行度はただ一つに決まります。
この時、系の組成はどうなっているのでしょうか。
系が平衡(正確には化学平衡)状態にあるときの反応商を\(K\)と表記することにします。この値は平衡定数として知られています。
図1の最小値をとる点が平衡状態で、このとき\(\Delta_\mathrm rG=0\)なので、次の式が成り立ちます。
\[
\Delta_\mathrm rG^\circ + RT \ln{K}=0
\]
\[
\Leftrightarrow K= \exp{\left( -\frac{\Delta_\mathrm rG^\circ}{RT} \right)}
\tag9
\]
自発変化の先には終着点がある
ここでもう一つ、私が勘違いしていたことをお話ししましょう。
よく演習問題で、教科書の裏にある各物質の標準生成ギブズエネルギーから標準反応ギブズエネルギーを求め、(9)式を用いて平衡定数を求めるという問題を見ますが、これを解いていてた過去の私は次のような疑問を抱いていました。
「標準反応ギブズエネルギー\(\Delta_\mathrm rG^\circ\)は負になれば自発的に反応する。なのに、なぜ平衡に達してしまうのだろう?」
言い換えれば、
「標準反応ギブズエネルギー\(\Delta_\mathrm rG^\circ\)は負で自発的に反応するはずなのに、反応が完全に進み切ることはなく、あるところで止まってしまうのはなぜなのだろう?」
これは、反応ギブズエネルギーが本来的にギブズエネルギーではないということに気づいていないがために陥ってしまった考えです。つまり、当時の私は、反応ギブズエネルギーというのは、反応が進んだときのギブズエネルギーのことだと勘違いしていました。
繰り返しになりますが、反応ギブズエネルギーは、生成ギブズエネルギーに化学両論係数をかけて足し合わせただけの値で、ギブズエネルギーを反応進行度で微分した時に現れる定数です。ギブズエネルギー自身ではないのです。
個人談
もしかすると、私が問題製作者の意図をくみ取れていないだけで、私が勝手に反応ギブズエネルギーとギブズエネルギーが等しいというような誤解をしていただけかもしれないと思い、教科書の後ろにある演習問題や演習書を見返したのですが、反応ギブズエネルギーとギブズエネルギーが等しいと思わせるような問題はありませんでした。
よくよく考えてみると、演習の授業で、教科書の後ろにあるような問題ではなく、先生が持ってきた問題を解いていた時にそのような勘違いに陥っていたと思い出しました。
演習問題は捨ててしまったので真相はわかりませんが、もしかしたら、先生の勘違いによって私自身も勘違いしていたのではないかと顧みます。
それはさておき、この記事を通して、反応ギブズエネルギーという極めて紛らわしい名称に騙される学生が一人でも少なくなってくれると、いいなぁと思います。
