無限に深い井戸型ポテンシャルとは
閉区間\([0, a]\)においてはポテンシャルが0で、他の領域ではポテンシャルが正の無限大であるような場合を考えてみましょう。
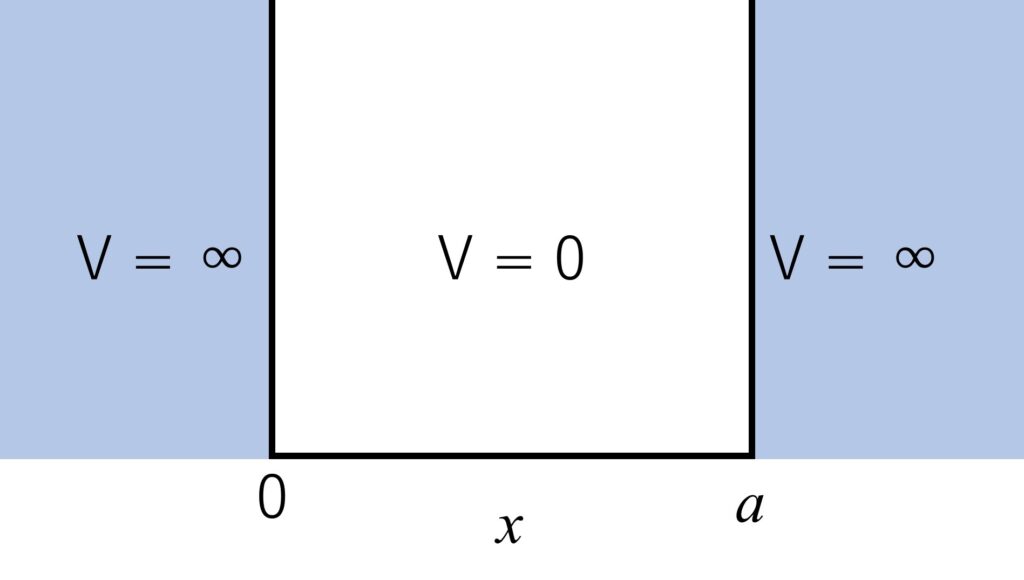
このような問題設定を、無限に深い井戸型ポテンシャル(particle in the box)といいます。
ポテンシャルが正の無限大であるとき、波動関数は0であることが必要です。なぜならば、波動関数が0以外の有限の値、あるいは無限大であると、シュレーディンガー方程式において\( V\psi= \infty\)となり、\(E\)が有限の値をとらないからです。
すなわち、\( \psi= 0\)として、\( V\psi\)を不定形にせざるを得ないのです。よって、\(\psi=0\)で、粒子の存在確率は0であることがわかります。
ここからは、\(0 \le x \le a\)として計算します。
取り得るエネルギーの計算
初めに、\(V=0\)であるときのシュレーディンガー方程式は次のようになります。
\[
\begin{align}
& – \frac{\hbar^2}{2m} \frac{d^2}{dx^2}\psi = E \psi \\[5pt]
\Leftrightarrow &\frac{d^2}{dx^2}\psi = -\frac{2mE}{\hbar^2}\psi
\end{align}
\]
これは、\(\psi\)を二階微分すると\(-2mE/\hbar^2\)という負の定数と\(\psi\)の掛け算が返ってくるということですが、これを満たす\(\psi\)はすぐに検討が着きます。
これは、\(\sin{kx}\)や\(\cos{kx}\)です。ここで、\(k = \sqrt{2mE / \hbar} \geq 0\)と置きました。このような形の微分方程式の一般解は、定数\(A\)、\(B\)を用いて次のようになることが知られています。
\[
\psi = A \cos{kx} + B \sin{kx} \tag1
\]
また、\(x=0, a\)では\( \psi(x) = 0\)です。これを境界条件と言います。これは、波動関数が連続であるという仮定を保証するためのものです。なぜ波動関数が連続であると仮定するかは省略します。
\[
\begin{cases}
\psi(0)=0\\
\psi(a)=0
\end{cases}
\]
よって、(1)について次の式が成り立ちます。
\[
\begin{align}
&
\begin{cases}
\psi(0) = A \cos 0 + B \sin 0 = 0 \\
\psi(a) = A \cos{ka} + B \sin{ka} = 0
\end{cases} \\
\Leftrightarrow
&\begin{cases}
A = 0 \\
B \cos{ka} = 0
\end{cases} \\
\Leftrightarrow
&\begin{cases}
A = 0 \\
B = 0 \quad \mathrm {or} \quad \cos{ka} = 0
\end{cases}
\end{align}
\]
ここで、\(B=0\)とすると、\(x\)に依らず\(\psi = 0\)となり、物理的に興味のない解となります。そのため、\(B\neq0\)とします。よって、
\[
\begin{align}
\cos{ka} &= 0 \\
ka &= n\pi \quad (n = 1,2,\cdots)\
\Leftrightarrow k &= \frac{n\pi}{a}
\end{align}
\]
\(n=0\)を入れなかった理由を説明します。\(n=0\)が解として含まれるとすると、\(ka=0\)となり、\(a\neq0\)なので\(k=0\)となります。
すると、全ての\(n=0\)に対して\(\cos{ka}=0\)、つまり\(\psi=0\)となり、やはり物理的に興味のない解になります。そのため、\(n=0\)を入れませんでした。
最後に、\(k\)の定義から、
\[
\begin{align}
&k = \frac{n\pi}{a}= \frac{\sqrt{2mE}}{\hbar} \\
\Rightarrow & E_n = \frac{h^2}{8ma}n^2
\end{align}
\]
\(E\)は\(n\)の関数なので\(E_n\)と表記しました。これを見ると、粒子のエネルギーは連続的な値をとらず、とびとびであることが分かります。
これは、整数\(n\)が含まれているからで、ボーアの量子条件で恣意的に取り入れたのとは違って、シュレーディンガー方程式を用いることによって、自然に現れました。
改めて、波動方程式は次のようになります。
\[
\psi = B \sin{ \frac{n\pi}{a} x}
\]
\(0\)から\(a\)の範囲で粒子が見つかる確率は1だから、次の式が成り立ちます。この操作は、波動関数の規格化といいます。
\[
\int_0^a{\psi^* \ \psi } \, dx = 1
\]
ここで、
\[
\begin{align}
\int_0^a{\sin^2{\frac{n\pi}{a}x}\, dx} &= \int_0^a{ \frac{1-2\cos{2\frac{n\pi}{a}x}}{2} \, dx} \\
&=
\left[
\frac{1}{2}x
\right]_0^a
–
\left[
\frac{a}{n\pi} \sin{2\frac{n\pi}{a}x}
\right]_0^a \\
&= \frac{a}{2} – \frac{a}{n\pi}
\left(
\sin{2n\pi}- \sin{0}
\right) \\
&= \frac{a}{2}
\end{align}
\]
よって、
\[
B^2 \int_0^a{ \sin^2{ \frac{n\pi}{a}x} \, dx} = B^2 \cdot \frac{a}{2}=1
\]
\[
B = \sqrt{\frac{2}{a}}
\]
ここで、本来ならば\(B=\pm\sqrt{\frac{2}{a}}\)になるはずです。ここで細かいことは説明しませんが、量子力学の仮説で、プラスでもマイナスでもどちらでもよいとしているので、ここではプラスの値を選びました。
3次元へ拡張
辺の長さがそれぞれ\(a, b, c\)の直方体\(D\)を考えます。この直方体について、原点に頂点をおき、\(x\)軸の値が\(0\)から\(a\)、\(y\)軸の値が\(0\)から\(b\)、\(z\)軸の値が\(0\)から\(c\)に辺が乗るようにします。
\(D\)でのポテンシャルは\(0\)で、外部では無限大であるとします。これは3次元の井戸型ポテンシャル、または箱型ポテンシャルと言われるものです。
この空間に粒子が存在するとき、シュレーディンガー方程式は次のようになります。
\[
-\frac{\hbar^2}{2m}
\left\{
\left(
\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}
\right)
+ V
\right\}
\psi=E\psi \tag2
\]
また、\(\psi(x,y,z)\)と書くと、境界条件は次のようになります。
\[
\begin{cases}
\psi(0, y, z) = \psi(a, y, z) = 0 \\[5px]
\psi(x, 0, z) = \psi(x, b, z) = 0 \\[5px]
\psi(x, y, 0) = \psi(x, y, c) = 0 \\[5px]
\end{cases}
\]
\(V \rightarrow \infty\)のとき、やはり\(\psi \to 0\)ですので、以降では領域\(D\)内について考えます。
\(V=0\)のとき、(2)式は次のようになります。
\[
-\frac{\hbar^2}{2m}
\left(
\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}
\right)
\psi
=E\psi \tag3
\]
これを解くために、\(\psi\)が次のように変数分離できると仮定します。
\[
\psi(x,y,z) = X(x)Y(y)Z(z) \tag4
\]
(4)式を(3)式に代入して、両辺\(XYZ\)で割ると、次のようになります。
\[
-\frac{\hbar^2}{2m}
\left(
\frac{1}{X}\frac{d^2 X}{dx^2} +
\frac{1}{Y}\frac{d^2 Y}{dy^2} +
\frac{1}{Z}\frac{d^2 Z}{dz^2}
\right)
= E \\
\]
ここで\(E_x, E_y, E_z\)は定数でなければらない理由を説明します。\(x, y, z\)は独立変数です。そのため、例えば\(E_x\)が\(x\)についての関数であったら、\(E_y\)や\(E_z\)は、\(E_x+E_y+E_z=E\)という足し算で\(E_x\)と紐づけられているので、これらも\(x\)の関数となります。
しかし、\(E_y\)や\(E_z\)は明らかにそれぞれ\(y\), \(z\)のみの関数または定数なので、\(E_x\)が\(x\)についての関数であることに矛盾します。
よって、\(E_x\)は定数であることが分かります。同様に、\(E_y\)や\(E_z\)も定数であることが分かります。
(5)式の微分方程式は1次元の無限に深い井戸型ポテンシャルで解きました。その時と同様に解くと、次のようになります。
\[
\begin{cases}
X=A_x \sin{ \frac{n_x \pi}{a} x } \quad &(n_x = 1,2,\cdots)\\
Y=A_y \sin{ \frac{n_y \pi}{b} y } \quad &(n_y= 1,2,\cdots) \\
Z=A_z \sin{ \frac{n_z \pi}{c} z } \quad &(n_z = 1,2,\cdots)
\end{cases}
\]
よって、シュレディンガー方程式は次のように書けます。
\[
\psi = A_x A_y A_z \sin{ \frac{n_x \pi}{a} x } \sin{ \frac{n_y \pi}{b} y } \sin{ \frac{n_z \pi}{c} z }
\]
波動関数を規格化して、
\[
\begin{align}
&\int_0^a{
\int_0^b{
\int_0^c{
{A_x}^2 {A_y}^2 {A_z}^2 \sin^2{ \frac{n_x \pi}{a} x } \sin^2{ \frac{n_y \pi}{b} y } \sin^2{ \frac{n_z \pi}{c} z} \, dxdydz
}
}
} \\
=& \int_0^a{
{A_x}^2 \sin^2{ \frac{n_x \pi}{a}} \, dx
}
\int_0^b{
{A_y}^2 \sin^2{ \frac{n_y \pi}{b}} \, dy
}
\int_0^c{
{A_z}^2 \sin^2{ \frac{n_z \pi}{c}} \, dz
}
=1\tag6
\end{align}
\]
応用: 共役系と吸収波長
有機化学で、共役アルケンの吸収波長において、炭素数が多いほど吸収波長は大きくなることを勉強したことはあるでしょうか。
この事実は、無限に深い井戸型ポテンシャルから導いた式から推察することができます。
共役系のπ電子は分子内に束縛されているため、共役系の外に出ようとすると電子は無限大のポテンシャルエネルギーを感じます。
これは井戸型ポテンシャルの設定と一致します(アルケンは直線ではないが、細かいことは気にしない)。さて、無限に深い井戸型ポテンシャルにおけるエネルギーの式をもう一度見てみましょう。
\[
E_n = \frac{h^2}{8ma}n^2
\]
この式を見ると、\(a\)が大きいほどエネルギーが小さくなることが分かります。
\(a\)は井戸の横幅でしたから、\(a\)が大きくなることは共役アルケンの炭素数が多くなることに等しいです。これにより、炭素数が多いほど吸収波長が長波長側にシフトすることが説明できます。
もっと言うと、なぜ共役アルケンは共役系を築いているのでしょうか。言い換えると、なぜ単結合と二重結合が交互にある構造ではないのでしょうか。
これも、上式から理解できます。この世界では、どういうわけだかエネルギーが小さい方に行きたがるため、2つの炭素間という狭い空間で二重結合を形成せず、共役系を形成して広い空間で電子を共有し、エネルギーを小さくしていると考えられます。
このように、無限に深い井戸型ポテンシャルや箱型ポテンシャルのような単純な系でも、共役についての定性的な説明ができるのです。
また、前述の通り縮退という量子力学で重要な結果も見ることができました。無限に深い井戸型ポテンシャルが初歩の量子化学で取り上げられるのは、このように様々な興味深い結論が多数得られるからです。いやー面白い。
