極限という概念は高校数学で学びますが、図形的、あるいは感覚的に身に着けている方が多いような気がします。本記事では、数式を用いた極限の厳密な定義について解説します。
極限とは
極限は主に数列の極限と関数の極限があります。ここでは、関数の極限について考えます。
関数の極限とは、変数がある値(極限)に限りなく近づく概念です。
例えば、関数\(f(x)\)について、\(x\)が\(a\)に限りなく近づくとき、極限値が\(L\)となることを次のように記述します。
\[
\lim_{x \to a} f(x)=L
\]
または、\(x \to a\)のとき\(f(x) \to L\)、あるいは\(f(x) \to L \ (x \to a)\)とも表記します。
極限のイメージと厳密な定義
こんなグラフを考えてみましょう。
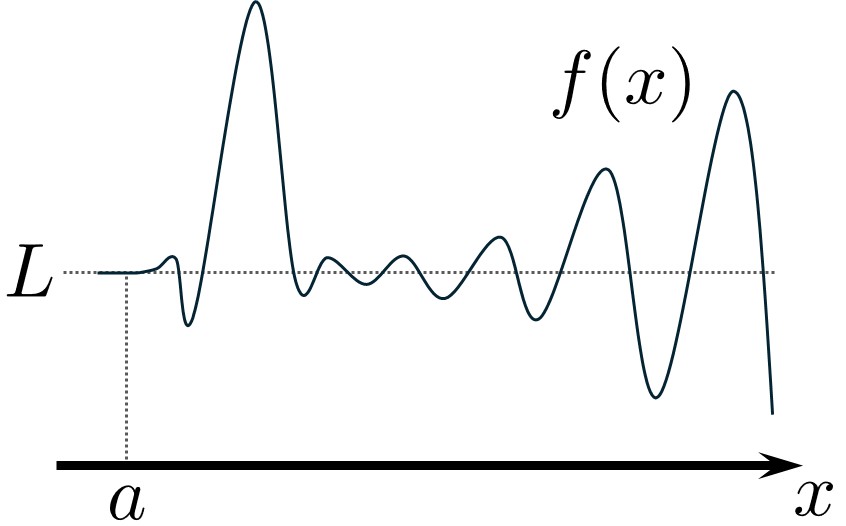
図からわかるように、\(f(x) \to L \ (x \to a)\)です。
さて、ある数\(\delta>0\)を用いて、\(x=a+\delta\)とし、\( \delta \)を\(0\)に近づけていくほど\(f(x)\)は\(L\)に近づくことを示せば極限を求めたということになります。
極限の定式化にあたって、「\( \delta \)を\(0\)に近づけていくほど\( f(x) \)は\(L\)に近づいていく」ことを数学的に表現してみたくなります。
しかし、これではなにかと不都合が生じます。
\(x\)を\(a\)に近づけていくとき、\(f(x)\)は上がったり下がったりします。つまり、\(\delta \)を徐々に\(0\)に近づけていくとき、あるところまでは\(f(x)\)が順調に\(L\)へと近づいていきますが、途中で突然\(f(x)\)が大きくなったり小さくなったりすることも場合によってはあります。
そのため、\( \delta \)を\(0\)に近づけていく過程で\(f(x)\)が極限値\(L\)から離れて行ってしまうこともあるため、このアイデアは使いにくいのです。
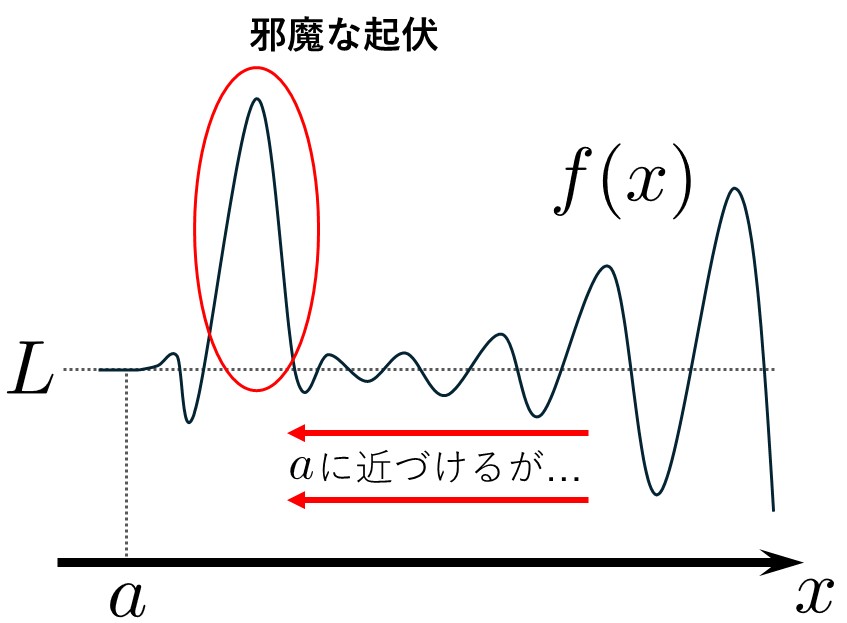
ここまでで、\(f(x)\)の起伏が厄介なことがわかりました。これをどうにかしなければなりません。
ここで、グラフに注目すると、起伏はあるにせよ、それを越えれば極限値\(L\)に着々と近づいていきます。この、起伏を無視して極限値\(L\)に着々と近づいている区間だけに目を向けたいわけです。
そのために、\(y\)の大きい部分を無視する仕組みを作ってみます。
\(\varepsilon>0\)を用いて、\( y =L -\varepsilon \)から\( y = L + \varepsilon \)の間に\(f(x)\)が収まるような\(x\)の範囲\((a, a+\delta)\)を探します。
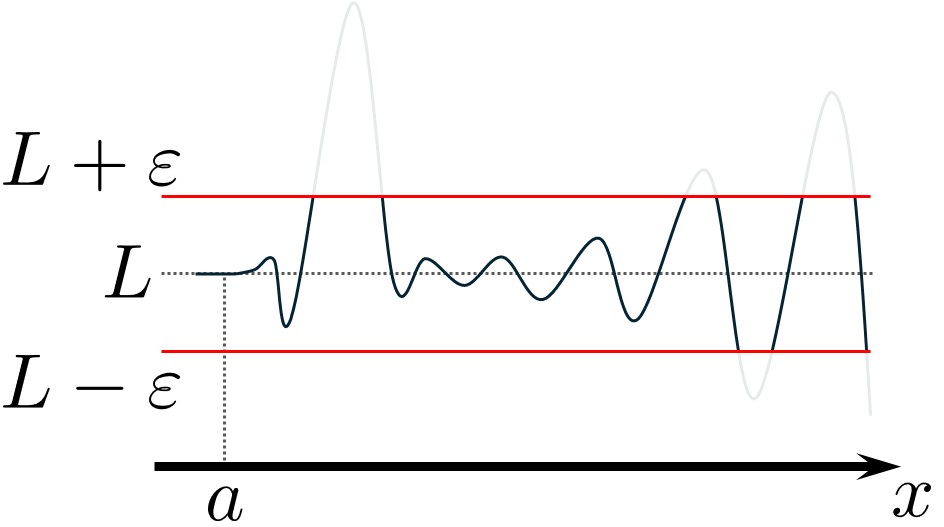
\( \varepsilon \)が起伏より小さくなるように設定すれば、厄介者の起伏を考えずに済みます。
また、\(\varepsilon\)を小さくしていけば、小さな起伏をも無視できるようになっていくのです。
このようにして、\(\varepsilon\)をいくら小さくしても、\(f(x)\)が収まるような区間\((a, a+\delta)\)が存在すれば、極限値は\(L\)であるといえるでしょう。
また、ここまでは\((a, a+\delta)\)の範囲で議論していましたが、\((a-\delta, a)\)でも同様に議論ができます。
このとき、\((a, a+\delta)\)で導かれる極限と、\((a-\delta, a)\)で導かれる極限はそれぞれ異なる場合があります。そのため、両者を区別する必要があります。
\((a, a+\delta)\)で導かれる極限を右極限、\((a-\delta, a)\)で導かれる極限を左極限といいます。
そして、右極限と左極限が一致するとき、それらを単に極限と呼びます。
まとめると、\(\varepsilon\)をいくらでも小さくしても、\(a-\delta<x<a+\delta\)すなわち\(|x-a|<\delta\)ならば\(|f(x)-L|<\varepsilon\)を満たすような\(\delta\)が存在するとき、\(L\)は極限といいます。
ただし、\(|x-a| \neq 0\)の範囲で考えたいので、\(0<|x-a|<\delta\)としましょう。
長くなりましたが、これで極限が定義できます。
\(f\)を\(a\)を含む開区間\(I\)で定義されている関数とする。ただし、\(f\)は\(a\)で定義されていなくてもよい。このとき、任意の\(\varepsilon(>0)\)に対して、
\[
0<|x-a|<\delta \Rightarrow |f(x)-L|<\varepsilon
\]
となる\(\delta(>0)\)が存在するとき、\(L\)は\(x\)が\(a\)に近づくときの\(f(x)\)の極限であるといい、このことを
\[
\lim_{x\to a} f(x)=L
\]
と書く。
また、任意の\(\varepsilon(>0)\)に対して、
\[
a<x<a+\delta \Rightarrow |f(x)-L|<\varepsilon
\]
となる\(\delta(>0)\)が存在するとき、\(L\)は\(x\)が\(a\)に近づくときの\(f(x)\)の右極限であるといい、このことを
\[
\lim_{x\to a^+} f(x)=L
\]
と書く。
さらに、任意の\(\varepsilon(>0)\)に対して、
\[
a-\delta<x<a \Rightarrow |f(x)-L|<\varepsilon
\]
となる\(\delta(>0)\)が存在するとき、\(L\)は\(x\)が\(a\)に近づくときの\(f(x)\)の左極限であるといい、このことを
\[
\lim_{x\to a^-} f(x)=L
\]
と書く。
\[
\lim_{x\to a^+} f(x)=\lim_{x\to a^-} f(x)=L \Longleftrightarrow \lim_{x\to a} f(x)= L
\]
は定義から容易に導かれる。
具体例(跳躍不連続点)
では、具体例を通して理解を深めましょう。
\[
f(x)=
\begin{cases}
2x+1 & (x \neq 2)\\
6 & (x=2)
\end{cases}
\]
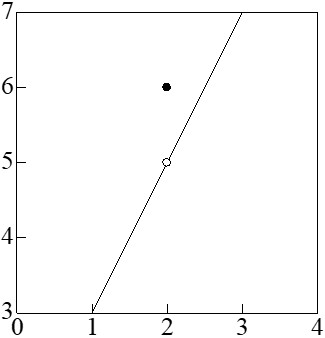
\(x\)が\(2\)に限りなく近づく時の極限はいくつになるでしょうか。
ポイントは、\(x\)は\(2\)に近づくが、\(2\)にはならないということです。
したがって、極限の定義を使わずとも、極限が\(5\)なりそうなのは図形的にわかります。
したがって、極限を\(5\)と仮定して、定義と矛盾がないかを確認していきます。
\[
\begin{align}
&|(2x+1)-5|<\varepsilon \\ \Longleftrightarrow
&|2x-4|<\varepsilon \\ \Longleftrightarrow
&|x-2|<\frac{\varepsilon}{2}
\end{align}
\]
よって、\(\delta=\varepsilon/2\)となるように\(\delta\)をとれば、極限の定義で示されている命題はいつも真となります。
つまり、
\[
\begin{align}
|x-2| < \frac{\varepsilon}{2} &\Longrightarrow 2|(x-2)| < \varepsilon \\
&\Longleftrightarrow |(2x+1)-5|<\varepsilon
\end{align}
\]
無限とは
\(f(x)=\displaystyle \frac{1}{x}\)とし、\(x \to 0\)の極限を考えます。\(x\)を0に近づけていくほど、\(f\)は大きくなっていきます。どこかの値に落ち着くするということはなさそうです。
これがいわゆる無限です。
\(f\)を\(a\)を含む開区間\(I\)で定義されている関数とする。ただし、\(f\)は\(a\)で定義されていなくてもよい。このとき、任意の\(M(>0)\)に対して、
\[
0<|x-a|<\delta \Longrightarrow f(x)>M
\]
となる\(\delta(<0)\)が存在するとき、\(x\)が\(a\)に近づくとき\(f(x)\)は正の無限大に発散するといい、このことを
\[
\lim_{x\to a} f(x)=\infty
\]
と記す。
また、
\[
0<|x-a|<\delta \Longrightarrow f(x)<M
\]
となる\(\delta(<0)\)が存在するとき、\(x\)が\(a\)に近づくとき\(f(x)\)は負の無限大に発散するといい、このことを
\[
\lim_{x\to a} f(x)=-\infty
\]
と記す。
今度は、\(f(x)=\displaystyle \frac{1}{x}\)において\(x\)を限りなく大きくしてみましょう。\(f(x)\)は\(0\)に近づいていくことがわかるかと思います。
\(f\)を区間\((a, \infty)\)で定義されている関数とする。任意の\(\varepsilon(>0)\)に対して、ある数\(N\)が存在して、
\[
x>N \Longrightarrow |f(x)-L|<\varepsilon
\]
であるとき、\(x\)が限りなく大きくなるとき\(f(x)\)は\(L\)に収束するといい、このことを
\[
\lim_{x\to \infty} f(x)=L
\]
と記す。
\(f\)を区間\((-\infty, a)\)で定義されている関数とする。任意の\(\varepsilon(>0)\)に対して、ある数\(N\)が存在して、
\[
x<N \Longrightarrow |f(x)-L|<\varepsilon
\]
であるとき、\(x\)が限りなく小さくなるとき\(f(x)\)は\(L\)に収束するといい、このことを
\[
\lim_{x\to -\infty} f(x)=L
\]
と記す。
今度は、\(g=a^x(a>0)\)を考えます。\(x\)を限りなく大きくしていくと、それに伴って\(g(x)\)も限りなく大きくなります。
この場合も先ほどと同じように極限を定義してみましょう。
\(f\)を区間\((a, \infty)\)で定義されている関数とする。任意の\(M(>0)\)に対して、ある数\(N\)が存在して、
\[
x>N \Longrightarrow f(x)>M
\]
であるとき、\(x\)が限りなく大きくなるとき\(f(x)\)は正の無限大に発散するといい、このことを
\[
\lim_{x\to \infty} f(x)=\infty
\]
と記す。
\(f\)を区間\((a, \infty)\)で定義されている関数とする。任意の\(M(>0)\)に対して、ある数\(N\)が存在して、
\[
x>N \Longrightarrow f(x)<M
\]
であるとき、\(x\)が限りなく大きくなるとき\(f(x)\)は負の無限大に発散するといい、このことを
\[
\lim_{x\to \infty} f(x)=-\infty
\]
と記す。
\(f\)を区間\((-\infty, a)\)で定義されている関数とする。任意の\(M(>0)\)に対して、ある数\(N\)が存在して、
\[
x<N \Longrightarrow f(x)>M
\]
であるとき、\(x\)が限りなく小さくなるとき\(f(x)\)は正の無限大に発散するといい、このことを
\[
\lim_{x\to -\infty} f(x)=\infty
\]
と記す。
\(f\)を区間\((-\infty, a)\)で定義されている関数とする。任意の\(M(>0)\)に対して、ある数\(N\)が存在して、
\[
x<N \Longrightarrow f(x)<M
\]
であるとき、\(x\)が限りなく小さくなるとき\(f(x)\)は負の無限大に発散するといい、このことを
\[
\lim_{x\to -\infty} f(x)=-\infty
\]
と記す。
はさみうちの原理
\(a\)を含む開区間\(I\)で\(f(x)\leq g(x)\leq h(x)\)であるとき、
\[
\lim_{x \to a} f(x) = \lim_{x \to a} h(x) = L \Longrightarrow \lim_{x \to a} g(x) = L
\]
区間\((a, \infty)\)で\(f(x)\leq g(x)\leq h(x)\)であるとき、
\[
\lim_{x \to \infty} f(x) = \lim_{x \to \infty} h(x) = L \Longrightarrow \lim_{x \to \infty} g(x) = L
\]
区間\((-\infty, a)\)で\(f(x)\leq g(x)\leq h(x)\)であるとき、
\[
\lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} h(x) = L \Longrightarrow \lim_{x \to -\infty} g(x) = L
\]
証明を表示
任意の\(\varepsilon>0\)に対して、
\[
0<|x-a|<\delta_1 \Longrightarrow |f(x)-L| < \varepsilon
\]
\[
0<|x-a|<\delta_2 \Longrightarrow |h(x)-L| < \varepsilon
\]
を満たすある\(\delta_1>0, \delta_2>0\)が存在する。\(\delta = \min(\delta_1, \delta_2)\)とすると、
\[
\begin{align}
0<|x-a|<\delta &\Longleftrightarrow
\begin{cases}
0<|x-a|<\delta_1\\
0<|x-a|<\delta_2\\
\end{cases} \\
&\Longrightarrow
\begin{cases}
|f(x)-L| < \varepsilon\\
|h(x)-L| < \varepsilon\\
\end{cases} \\
& \Longrightarrow
-\varepsilon < f(x)-L \leq g(x)-L \leq h(x)-L < \varepsilon \\
&\Longrightarrow -\varepsilon < g(x)-L < \varepsilon \\
&\Longleftrightarrow |g(x)-L|<\varepsilon
\end{align}
\]
は真である。
任意の\(\varepsilon>0\)に対して、
\[
x>N_1 \Longrightarrow |f(x)-L| < \varepsilon
\]
\[
x>N_2 \Longrightarrow |h(x)-L| < \varepsilon
\]
を満たすある\(N_1>0, N_2>0\)が存在する。\(N = \min(N_1, N_2)\)とすると、
\[
\begin{align}
x>N &\Longleftrightarrow
\begin{cases}
x>N_1\\
x>N_2\\
\end{cases} \\
&\Longrightarrow
\begin{cases}
|f(x)-L| < \varepsilon\\
|h(x)-L| < \varepsilon\\
\end{cases} \\
& \Longrightarrow
-\varepsilon < f(x)-L \leq g(x)-L \leq h(x)-L < \varepsilon \\
&\Longrightarrow -\varepsilon < g(x)-L < \varepsilon \\
&\Longleftrightarrow |g(x)-L|<\varepsilon
\end{align}
\]
は真である。
任意の\(\varepsilon>0\)に対して、
\[
x<N_1 \Longrightarrow |f(x)-L| < \varepsilon
\]
\[
x<N_2 \Longrightarrow |f(x)-L| < \varepsilon
\]
を満たすある\(N_1>0, N_2>0\)が存在する。\(N = \max(N_1, N_2)\)とすると、
\[
\begin{align}
x<N &\Longleftrightarrow
\begin{cases}
x<N_1\\
x<N_2\\
\end{cases} \\
&\Longrightarrow
\begin{cases}
|f(x)-L| < \varepsilon\\
|h(x)-L| < \varepsilon\\
\end{cases} \\
& \Longrightarrow
-\varepsilon < f(x)-L \leq g(x)-L \leq h(x)-L < \varepsilon \\
&\Longrightarrow -\varepsilon < g(x)-L < \varepsilon \\
&\Longleftrightarrow |g(x)-L|<\varepsilon
\end{align}
\]
は真である。
極限の公式
極限の四則演算にはわかりやすい公式があります。
\(\displaystyle \lim_{x \to a}f(x)=L, \lim_{x \to a}g(x)=M\)が存在するなら、次式が成り立つ。ただし、\(a\)は\(\infty, -\infty\)としてもよい。
\[
\begin{align}
\lim_{x \to a}(f(x) \pm g(x))= L \pm M && (複合同順) \tag1
\end{align}
\]
\[
\lim_{x \to a}(f(x)g(x))= LM \tag2
\]
\[
\begin{align}
\lim_{x \to a}\frac{f(x)}{g(x)}= \frac{L}{M} && (M \neq 0) \tag3
\end{align}
\]
\[
\begin{align}
\lim_{x \to a}c = c && (c=\text{const.}) \tag4
\end{align}
\]
(1)の証明を表示
任意の\(\varepsilon/2 >0\)に対して、
\[
0<|x-a|<\delta_1 \Longrightarrow |f(x)-L| < \frac{\varepsilon}{2}
\]
\[
0<|x-a|<\delta_2 \Longrightarrow |\pm g(x)-M| < \frac{\varepsilon}{2}
\]
を満たす\(\delta_1, \delta_2\)が存在する。
いま、三角不等式\(|x+y| \leq |x|+|y|\)を用いて、\(\delta = \min(\delta_1, \delta_2)\)とすると
\[
\begin{alignat}{3}
0<|x-a|&<\delta&
\Longrightarrow&
\begin{cases}
0<|x-a|<\delta_1 \\
0<|x-a|<\delta_2
\end{cases}
\\
&&
\Longrightarrow&
\begin{cases} \displaystyle{
|f(x)-L| < \frac{\varepsilon}{2} \\
|g(x)-M| < \frac{\varepsilon}{2}
}
\end{cases} &
\Longrightarrow&
|f(x) \pm g(x)-(L+M)| \\
&&&&
=&|(f(x)-L) + (\pm g(x)-M)|\\
&&&&
\leq &|f(x)-L|+|( \pm g(x)-M)| \\
&&&&
<& \frac{\varepsilon}{2} + \frac{\varepsilon}{2}=\varepsilon
\end{alignat}
\]
(2)の証明を表示
任意の\(\varepsilon>0\)に対して、
\[
0<|x-a|<\delta_1 \Longrightarrow |g(x)-M| < \frac{\varepsilon}{2|L|} \tag{2.1}
\]
\[
0<|x-a|<\delta_2 \Longrightarrow |g(x)-M| < 1 \tag {2.2}\\
\]
\[
0<|x-a|<\delta_3 \Longrightarrow |f(x)-L| < \frac{\varepsilon}{2(1+|M|)} \tag {2.3}
\]
を満たす\(\delta_1, \delta_2, \delta_3\)が存在する。
三角不等式を用いて、
\[
(2.2) \Longrightarrow |g(x)| = |g(x)-M+M| \leq |g(x)-M|+|M| < 1+|M| \tag{2.4}
\]
したがって、\(\delta=\min \{ \delta_1, \delta_2, \delta_3 \} \)とすれば、\((2.1), (2.2), (2.3), (2.4)\)式より、
\[
0<|x-a|<\delta
\Longleftrightarrow
\begin{cases} \displaystyle{
0<|x-a|<\delta_1 \Longrightarrow |g(x)-M| < \frac{\varepsilon}{2|L|} \\
0<|x-a|<\delta_2 \Longrightarrow |g(x)-M| < 1 \Longrightarrow |g|<1+|M| \\
0<|x-a|<\delta_3 \Longrightarrow |f(x)-L| < \frac{\varepsilon}{2(1+|M|)}
}
\end{cases}
\]
\[
\begin{align}
\Longrightarrow
|f(x)g(x)-LM| &=|f(x)g(x)-Lg(x)+Lg(x)-LM|\\
&= |g(x)(f(x)-L)+L(g(x)-M)| \\
& \leq |g(x)||(f(x)-L)|+|L||g(x)-M| \\
&<(1+|M|) \cdot \frac{\varepsilon}{2(1+|M|)}+|L|\cdot \frac{\varepsilon}{2|L|}\\
&=\varepsilon
\end{align}
\]
(3)の証明を表示
まず、\(\displaystyle \lim_{x \to a}\frac{1}{g(x)}=\frac{1}{M}\)を示す。
任意の\(\varepsilon>0\)に対して、
\[
0<|x-a|<\delta_1 \Longrightarrow |g(x)-M|<\frac{|M|}{2} \tag{3.1}
\]
\[
0<|x-a|<\delta_2 \Longrightarrow |g(x)-M|<\frac{M^2}{2}\varepsilon \tag{3.2}
\]
を満たす\(\delta_1, \delta_2\)が存在する。
三角不等式を用いて、
\[
(3.1) \Longrightarrow |M| = |M – g(x) + g(x)| \leq |M-g(x)| + |g(x)| < \frac{|M|}{2} +|g(x)|
\]
\[
\Longleftrightarrow \frac{1}{|Mg(x)|}<\frac{2}{M^2} \tag{3.3}
\]
したがって、\(\delta=\min \{ \delta_1, \delta_2 \} \)とすれば、\((3.1), (3.2), (3.3)\)より、
\[
\begin{align}
\begin{cases}
0<|x-a|<\delta_1\\
0<|x-a|<\delta_2
\end{cases}
\Longrightarrow
0<|x-a|<\delta
\Longrightarrow
\left| \frac{1}{g(x)}-\frac{1}{M} \right|&=\frac{|M-g(x)|}{|Mg(x)|} \\
&<\frac{\displaystyle \frac{M^2}{2}\varepsilon}{\displaystyle \frac{M^2}{2}} \\
&=\varepsilon
\end{align}
\]
以上で、\(\displaystyle \lim_{x \to a}\frac{1}{g(x)}=\frac{1}{M}\)が示された。
続いて、定理の(2)式を用いて、
\[
\begin{align}
\lim_{x \to a}\frac{f(x)}{g(x)} &= \lim_{x \to a}{f(x)} \cdot \lim_{x \to a}\frac{1}{g(x)}\\
&=\frac{L}{M}
\end{align}
\]
(4)の証明を表示
任意の\(\varepsilon>0\)に対して、命題\[
0<|x-a|<\delta \Longrightarrow |c-c|=0<\varepsilon
\]
は、任意の\(\delta>0\)で真である。
