平均値の定理は、微分学における重要な命題を導くために必要な道具です。また、微分と積分をつなぐ重要な定理でもあります。
証明の準備
平均値の定理を証明する前に、いくつか定義や定理を紹介する必要があります。
最大値・最小値の定義
初めに、最大値と最小値の定義です。
\(c\)を関数\(f\)の定義域\(D\)内の数とする。任意の\(x \in D\)について、
- \(f(c)\geq f(x)\)であるとき、\(f(c)\)は\(f\)の最大値である。
- \(f(c)\leq f(x)\)であるとき、\(f(c)\)は\(f\)の最小値である。
極値(極大値・極小値)の定義
続いて、極大値と極小値です。
関数\(f\)の定義域\(D\)内にある数\(c\)に対して、ある数\(\varepsilon>0\)が存在して定義域\(D\)内で\(c-\varepsilon < x < c + \varepsilon\)ならば、
- \(f(c)\geq f(x)\)であるとき、\(f(c)\)は\(f\)の極大値である。
- \(f(c)\leq f(x)\)であるとき、\(f(c)\)は\(f\)の極小値である。
また、極大値あるいは極小値のことを単に極値ともいう。
ちなみに、ある数\(c\)に対して、ある数\(\varepsilon>0\)が存在して定義域\(D\)内で\(c-\varepsilon < x < c + \varepsilon\)という領域(集合)は、\(c\)の近傍と表現されます。
最大値・最小値および極値の定義は、どちらも納得のいくものかと思います。
また、極大かつ最大、あるいは極小かつ最小という場合もあります。
ただし、最大値or最小値だからといって、必ずしも極値にはなりませんし、極値だからと言って必ずしも最大値or最小値にはなりません。
最大値・最小値の定理
さて、最大値・最小値について、次のような定理があります。
閉区間\([a, b]\)で連続な関数\(f\)は、区間\([a, b]\)内にある数\(c, d\)が存在して、\(f(c), f(d)\)はそれぞれ最大値と最小値である。
証明は骨が折れるので割愛します。実際、ほとんどの初等的な微分積分学の教科書でも、最大値・最小値の定理を認めるスタンスをとっています。
少し頭の中で想像していただければ、この定理が当たり前なことは容易に分かるかと思います。
極値の定理
関数\(f\)が\(c\)で極値をとり、\(f'(c)\)が存在するならば、\(f'(c)=0\)
証明を表示
(i)\(f(c)\)が極大値をとるとき、
極大値の定義より、
\[
\begin{align}
f(c) \geq f(c+h) &\Longleftrightarrow f(c+h) – f(c) \leq 0 \\
&\Longleftrightarrow
\begin{cases}
\displaystyle \frac{f(c+h) – f(c)}{h} \leq 0 & (h>0)\\
\displaystyle \frac{f(c+h) – f(c)}{h} \geq 0 & (h<0)
\end{cases} \\
&\Longrightarrow
\begin{cases}
\displaystyle \lim_{x \to 0^+} \frac{f(c+h) – f(c)}{h} = f'(c) \leq 0 & (h>0)\\
\displaystyle \lim_{x \to 0^-} \frac{f(c+h) – f(c)}{h} = f'(c) \geq 0 & (h<0)
\end{cases} \\
&\Longleftrightarrow f'(c)=0
\end{align}
\]
まとめると、
\[
f(c) \geq f(c+h)\Longrightarrow f'(c)=0
\]
(ii)\(f(c)\)が極小値をとるとき、
極小値の定義より、
\[
\begin{align}
f(c) \leq f(c+h) &\Longleftrightarrow f(c+h) – f(c) \geq 0 \\
&\Longleftrightarrow
\begin{cases}
\displaystyle \frac{f(c+h) – f(c)}{h} \geq 0 & (h>0)\\
\displaystyle \frac{f(c+h) – f(c)}{h} \leq 0 & (h<0)
\end{cases} \\
&\Longrightarrow
\begin{cases}
\displaystyle \lim_{x \to 0^+} \frac{f(c+h) – f(c)}{h} = f'(c) \geq 0 & (h>0)\\
\displaystyle \lim_{x \to 0^-} \frac{f(c+h) – f(c)}{h} = f'(c) \leq 0 & (h<0)
\end{cases} \\
&\Longleftrightarrow f'(c)=0
\end{align}
\]
まとめると、
\[
f(c) \leq f(c+h)\Longrightarrow f'(c)=0
\]
以上より、題意は示された。
これも、証明を見ずとも直感的に納得できる定理かと思います。
ロルの定理(Rolleの定理)
関数\(f\)は閉区間\([a, b]\)で連続、開区間\((a, b)\)で微分可能、\(f(a)=f(b)\)であるならば、\(f'(c)=0\)となる数\(c(a<c<b)\)が存在する。
証明を表示
(i)\(f\)が定数関数であるとき、明らかに\(\f'(c)=0)である。
(ii)ある数\(x(a<x<b)\)について、\(f(x) < f(a)\)であるとき、
定理1: 最大値・最小値の定理より、\(f\)は閉区間\([a,b]\)のある数\(c\)で最大値をとる。また、\(f(x) > f(a) = f(b)\)だから、\(f(a)\)と\(f(b)\)は最大値ではない。すなわち、\(a<c<b\)である。これより、\(f(c)\)は極大値でもある。したがって、定理2より、\(f'(c)=0\)
(iii)ある数\(x(a<x<b)\)について、\(f(x) > f(a)\)であるとき、
定理1: 最大値・最小値の定理より、\(f\)は閉区間\([a,b]\)のある数\(c\)で最小値をとる。また、\(f(x) < f(a) = f(b)\)だから、\(f(a)\)と\(f(b)\)は最小値ではない。すなわち、\(a<c<b\)である。これより、\(f(c)\)は極小値でもある。したがって、定理2より、\(f'(c)=0\)
以上より、ロルの定理が示された。
ロルの定理を図示すると次のようになります。
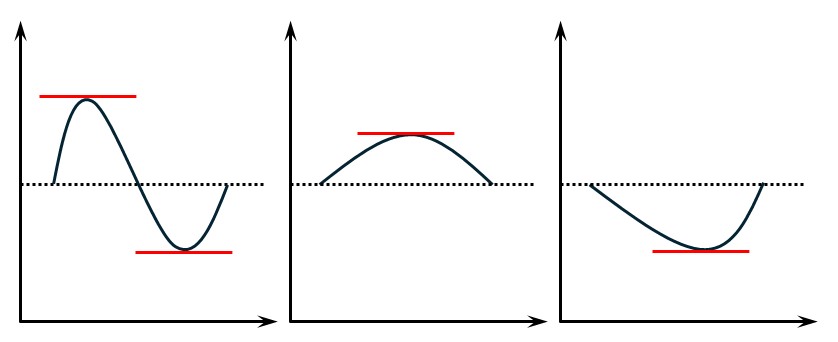
これも、直感的にわかりやすい定理かと思います。
平均値の定理(Lagrangeの平均値の定理)
ここで、こんな操作を施します。
ロルの定理が成り立つのなら、点\((a, f(a))\)と点\((b, f(b))\)を結ぶ線の傾きに等しい微分係数\(f'(c)\)となるような数\(c(a<c<b)\)が存在するでしょう。
これが、平均値の定理です。
関数\(f\)は閉区間\([a, b]\)で連続、開区間\((a, b)\)で微分可能であるならば、ある数\(c(a<c<b)\)が存在し、
\[
f'(c)=\frac{f(b)-f(a)}{b-a}
\]
証明の表示
図2からわかるように、\(f(x)\)から\((a, f(a))\)と\((b, f(b))\)を通る直線の式を引けば、ロルの定理が使える形になります。
関数\(h(x)\)を次のように定義する。
\[
h(x)=f(x)-f(a)-\frac{f(b)-f(a)}{b-a}(x-a)
\]
このとき、\(h(x)\)は連続な関数\(f\)と\(x\)の四則演算からなるため、\(h(x)\)は閉区間\([a, b]\)で連続、開区間\((a, b)\)で微分可能である。
また、
\[
h(a)=f(a)-f(a)-\frac{f(b)-f(a)}{b-a}(a-a)=0
\]
\[
h(b)=f(b)-f(a)-\frac{f(b)-f(a)}{b-a}(b-a)=0
\]
したがって、定理3: ロルの定理より、
\[
h'(c)=f'(c)-\frac{f(b)-f(a)}{b-a} = 0 \Longleftrightarrow f'(c)=\frac{f(b)-f(a)}{b-a}
\]
を満たすある数\(c(a<c<b)\)が存在する。
平均値の定理から導かれる重要な命題
\(C\)を定数とすると、\(f(x)=C \Longrightarrow f'(x)=0\)ですが、\(f'(x)=0\)となるような関数は\(f(x)=C\)以外に存在するのでしょうか?
この問いに対して、Noと答えるのが次の定理5になります。
開区間\((a, b)\)内のすべての\(x\)について\(f'(x)=0\)なら、\(f\)は区間\((a, b)\)で定数関数である。
証明を表示
\(x_1, x_2 (a<x_1<x_2<b)\)を、開区間\((a, b)\)内にある任意の数とする。\(f\)は\((a, b)\)で微分可能であるため、\((x_1, x_2)\)でも微分可能である。また、別の記事で示した定理より、\((x_1, x_2)\)で微分可能ならば\((x_1, x_2)\)で連続である。
よって、平均値の定理より、ある数\(c (x_1<c<x_2)\)が存在し、
\[
f'(c)=\frac{f(x_2)-f(x_1)}{x_2-x_1}=0 \Longleftrightarrow f(x_2)=f(x_1)
\]
この定理5を用いて、重要な命題(系6)を示します。
開区間\((a, b)\)内のすべての\(x\)について\(f'(x)=g'(x)\)ならば、ある定数\(C\)が存在し、区間\((a, b)\)で\(f(x)=g(x)+ C \)である。
証明を表示
\[
(f(x)-g(x))’=f'(x)-g'(x)=0
\]
よって、定理5より、
\[
f(x)-g(x)=C \Longrightarrow f(x)=g(x)+C
\]
例えば、\(C\)を定数として、\(f(x)=x^2 + C \Longrightarrow f'(x)= 2x\)ですが、\( g'(x)= 2x\)となるような関数は\(f(x)\)以外に存在しないというのが、系6の主張です。
さいごに
大学受験を経験している方なら分かるかと思いますが、大学入試の世界で平均値の定理は超難関大学の難しい問題でしか使われない定理なので、使い道が少ないと思われているかもしれません。
しかし、微分積分学では明確な役割があります。系6は、微分と積分をつなぐ定理である微分積分学の基本定理の証明に使います。
詳しくはこちらの記事をご覧ください。
