はじめに
原子の電子配置はマーデルングの規則に従うことが多いことを説明した記事があります。当記事は、その内容については理解していることを前提に進めますのでご了承ください。
まだご覧になっていない方はこちら。
周期表はうまくできている
そもそも、周期表にある元素の並びには意味があることをご存じでしょうか。以下に典型的な周期表を示します。
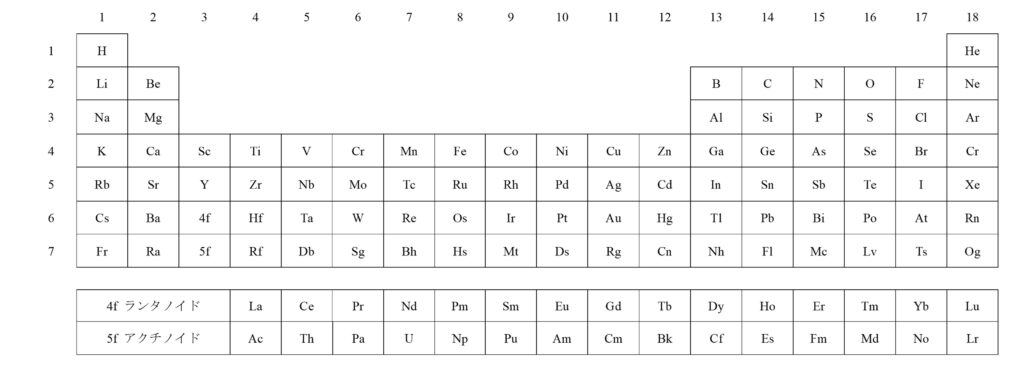
周期表のうち、第n列(つまり左からn番目の縦のライン)の元素のことを第n族元素といい、第m行(つまり上からm番目の横のライン)の元素のことを第m周期元素といいます。
また、各周期では左から右へ行くほど原子番号が1つずつ大きくなり、各族では上から下へ行くほど原子番号が大きくなります。
さらに、第m周期における18族元素の原子番号に1を足したものが第m+1周期における1族元素の原子番号になります。つまり、水素Hの原子番号を1として、He, Li, Be, B,…の順に原子番号が1ずつ増えていきます。
ここで注目してほしいのは、第一周期のHは1s軌道に1つ、Heは2つ電子が入り、その次に2s軌道に電子が1つ入る元素は第2周期のLiである点です。
主量子数が変わったところで周期も同時に変わりました。このように、主量子数と周期には密接な関係があります。同様に、2s, 2p軌道と電子を入れ、2p軌道に電子が6個入ったところで第2周期の第18族にたどり着きます。
ここからさらに電子を加えるとなると、主量子数が変わって3s軌道に入りますが、やはり今度は第3周期元素に移ります。このようなことがわかると、第1族と第2族の元素はs軌道に関連した元素であることがわかります。
よって、第1族と第2族の元素をsブロック元素と言います。同様にして、13から18族元素のことをpブロック元素と言います。ただし、Heは電子配置が1s2であるため、sブロック元素とみなします(以下の図2を参照)。
更に電子を3s, 3p軌道に加えていき、4s軌道に電子を入れるところで第4周期に入ってきます。4s軌道に2個電子が入ると、今度は3d軌道に電子が10個まで入ることになります。
また、これに相当する元素は3から12族元素のちょうど10個で、13族以降の元素は4p軌道に入っていくわけです。このため、3から12族元素のことをdブロック元素と言います。
なお、このまま電子を入れていくと、第6周期または第7周期の第3族でf軌道に電子が入るため、この部分だけ欄外にfブロック元素が描かれるのが普通です。
ここまでくると、周期表がよくできていることがわかると思います。

余談ですが、現在で最も原子番号の大きな元素はオガネソンOgです。これは第7周期第18族元素で周期表の一番右下にあります。
Ogは天然には存在せず、加速器という装置を用いて無理やり作られました。もし、これよりも大きい原子番号の元素が作られると、周期表が大変なことになります。第8周期に入り、8sに2つの電子を入れたら次はg軌道に電子を入れます。
g軌道とは、方位量子数4の軌道です。つまり、s, p, d, f軌道の次にg軌道がきます。このg軌道に入った電子を周期表ではどうやって表現するのだ、というのが問題になってくるわけです。ただでさえf軌道は欄外に書かれているのに、g軌道もそうするのかという話です。
もしgブロック元素の合成に成功したら、周期表は新たなデザインに変わるかもしれません。実際、新しいデザインの周期表を考えている方々もいらっしゃいます。
原子半径とイオン半径
周期表を見ると、原子半径とイオン半径をある程度予測することができます。
ボーアモデルでは、水素原子の半径は主量子数の2乗に比例して大きくなりますが、水素原子以外でも一般的に主量子数が大きくなると原子半径は大きくなります。
そのため、各族では周期表の下に行くほど原子半径は大きくなります。ボーアモデルについてはこちら。
では、同一周期上ではどのような法則があるのでしょうか。ここでは第3周期までで考えてみましょう。そうすると、同一周期では主量子数が変わらないため、先ほどのような議論はできません。
したがって、原子半径の大小に関係しそうな別のファクターを見つけなければなりません。ここで思い浮かべてほしいのは、静電気力です。
原子核は正の電荷を帯びており、電子は負の電荷をもちます。そのため、原子核の正電荷が大きくなると原子半径は小さくなりそうな気がしますが、原子番号が増えれば陽子数が増えると同時に電子数も増えるため、結局原子半径は変わらないのではないかと思うかもしれません。
しかし実際は、周期表の左から右に行くほど原子半径は小さくなります。
これは、原子番号の増加による電子の増加では、原子核の正電荷の増加を抑えきれないからです。例えば、原子番号10のネオンNeについて考えます。
最外殻電子以外の電子9個の電荷−9が10個の陽子の正電荷+10を打ち消して、事実上最外殻電子は原子核の電荷を+1であると感じるのではないかと考えられそうです。
しかし、実際には電子9個の寄与は−9よりも小さく、例えば−8くらいかもしれません。一見すると不思議に感じるかもしれませんが、次のような状況を考えれば理解できると思います。
例えば2px軌道の電子Aと2py電子Bがほぼ隣にいるとして、電子Aが感じる原子核の正電荷を考えると、電子Bは正電荷をあまり打ち消してくれていないため、電子Bは−1だけ電荷を打ち消すとは考えられません。
このように、電子は原子核の正電荷を完全には遮蔽しません。したがって、同一周期で原子番号が増えてゆくと電子は増える一方で、遮蔽できない正電荷が大きくなっていくため、周期表の左から右に行くにつれて原子半径は大きくなります。
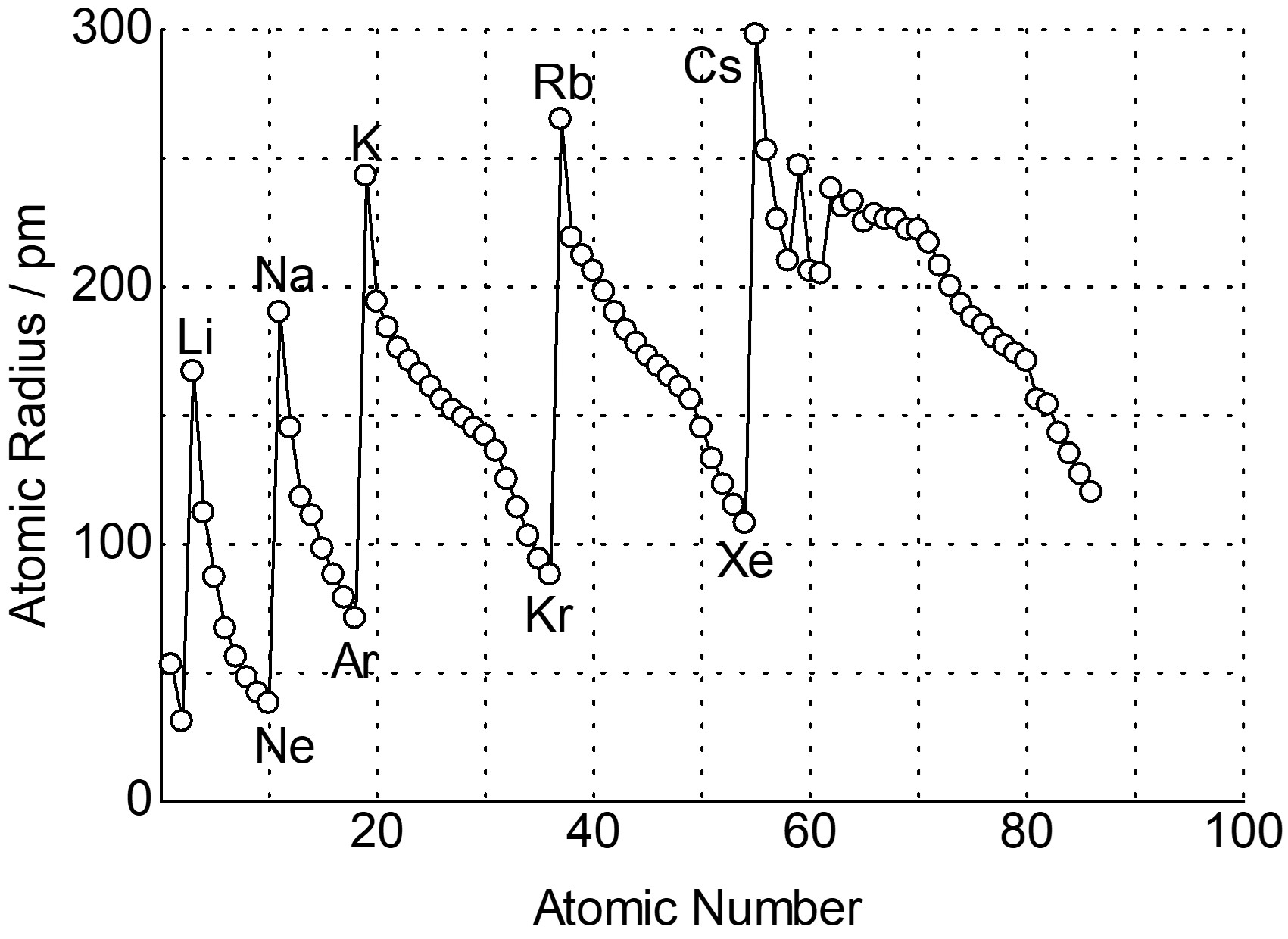
イオン半径についても同様の議論ができます。また、陽イオンは中性の同一原子に比べて例外なく小さく、陰イオンは大きいです。
これは単純に原子核の正電荷を考えればすぐにわかります。陽イオンは電子が少ない分だけ原子核がもつ正味の正電荷が大きくなり、陰イオンは電子が多い分だけ原子核がもつ正味の正電荷が小さくなるからです。
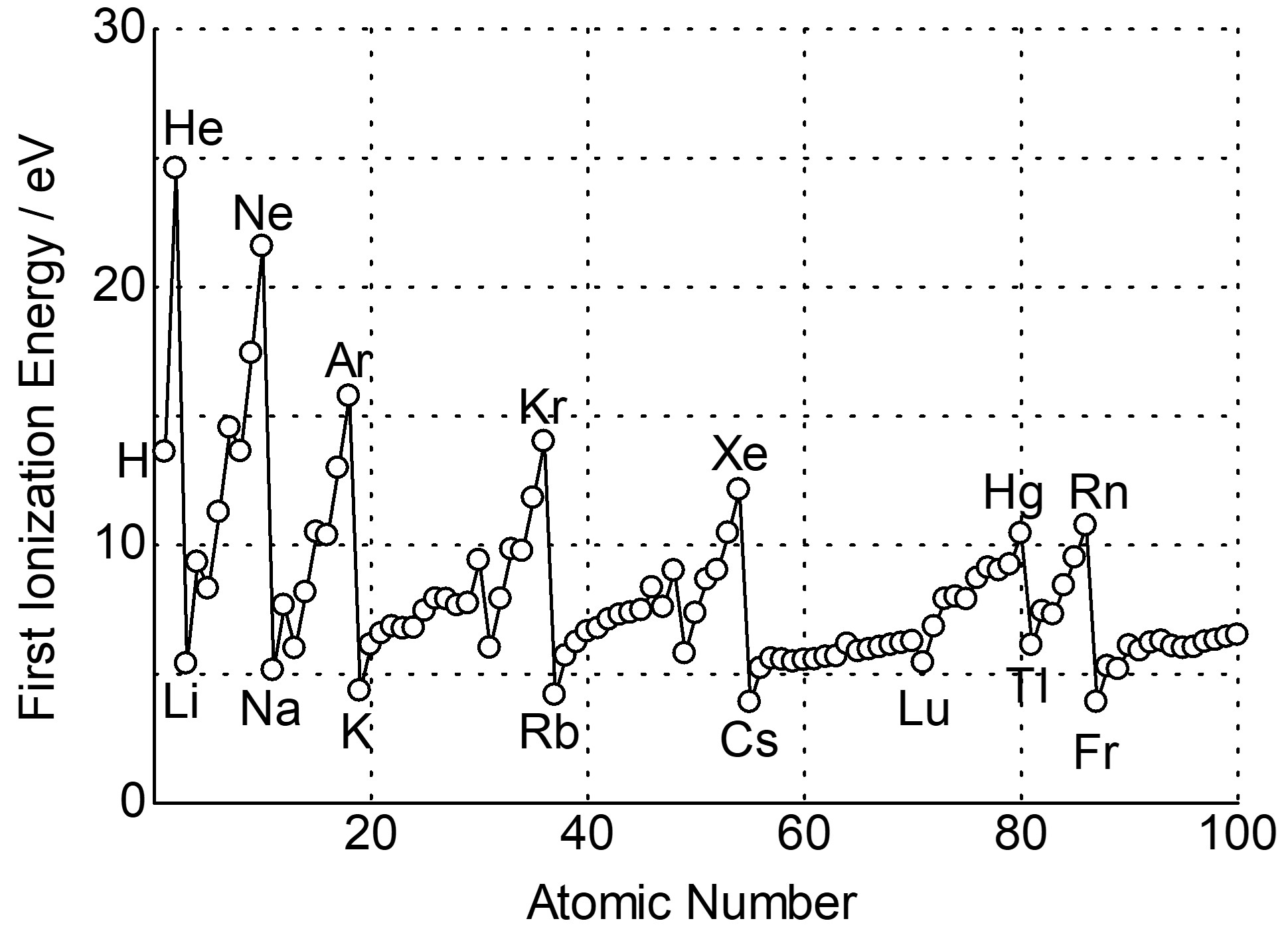
イオン化エネルギー
イオン化エネルギーとは、電子を取り去るのに必要なエネルギーです。特に、電子をn個とるのに必要なエネルギーを第nイオン化エネルギーと言います。
ボーアモデルを思い出すと、主量子数の大きな軌道のエネルギー準位は大きいことがわかりますが、これに関しても一般の原子で成り立ちます。
エネルギー準位の大きな軌道の電子は、エネルギー準位の小さな軌道の電子よりも不安定なため、容易にとることができます。したがって、同一族上で、周期表の上から下に行くにつれてイオン化エネルギーは小さくなります。
また、原子半径の議論で説明した遮蔽を思い出せば、同一周期におけるイオン化エネルギーの順列について予測できるはずです。
原子核の正味の正電荷が大きければそれだけ電子を引き付けていることになるため、イオン化エネルギーは大きくなります。
したがって、同一周期上で、周期表の左から右に行くにつれてイオン化エネルギーは大きくなります。