理想気体とは
理想気体とは、分子の大きさがなく、それらの相互作用が全て等しく、総じて0としてよいような気体のことを言います。
高温低圧では、気体は理想気体に近づき、次の理想気体の状態方程式をよく満たすことが知られています。
\[PV=nRT\]
ここで\(P\)は気体の圧力、\(V\)は気体の体積、\(n\)は気体の物質量、\(R\)は気体定数、\(T\)は気体の温度です。
また、モル体積\(\bar V=V/n\)を定義して次のようにも書けます。
\[P \bar V =RT\]
細かな話ですが、この式のいいところは変数がすべて示強性変数であるところです。
これらの式を満たすのは、理想気体のみです。さて、ここではボイルの法則とシャルルの法則、アボガドロの法則が成り立つ条件下で理想気体の状態方程式を導出してみます。
ただし、これら上記の法則は特定の条件下でしか成り立たないので、一般に理想気体の状態方程式が成り立つことまでは言えません。
ボイルの法則とは、温度と物質量が一定の条件で、次のような式が成り立つという主張です。
\[PV=const.\]
ここで\(const.\)は定数(constant)を意味します。
シャルルの法則とは、体積と物質量が一定の条件で、次のような式が成り立つという主張です。
\[\frac{P}{T}=const.\]
アボガドロの法則とは、圧力と温度が一定の条件で、次のような式が成り立つ法則です。
\[\frac{V}{n}=const.\]
まず、状態Aでの気体の圧力、体積、温度をそれぞれ\(P_1, V_1, T_1\)とします。次に、温度と物質量一定で\(P_2, V_2, T_1\)という状態Bにします。続いて、体積と物質量一定で、\(P_3, V_2, T_2\)という状態Cにします。最後に、圧力と温度一定で\(P_3, V_3, T_2\)という状態Dにします。
\[
A(P_1, V_1, T_1) \rightarrow
B(P_2, V_2, T_1) \rightarrow
C(P_3, V_2, T_2) \rightarrow
D(P_3, V_3, T_2)
\]
まずAからBへの変化では、ボイルの法則が成り立ちます。
\[
P_1 V_1 = P_2 V_2
\]
\[
\unicode{x2234} P_2 = P_1 \frac{V_1}{V_2} \tag 1
\]
次に、BからCへの変化では、シャルルの法則が成り立ちます。
\[
\frac{P_2}{T_1} = \frac{P_3}{T_1} \tag2
\]
(1)を(2)に代入して、
\[
P_1 \frac{V_1}{V_2} \frac{1}{T_1} = \frac{P_3}{T_2}
\]
\[
\unicode{x2234} \frac{P_1 V_1}{T_1} = \frac{P_3 V_2}{T_2}
\]
この式は、AとCの状態で記述されていることがわかります。これを、ボイル・シャルルの法則と言います。
最後に、圧力と体積一定下では、アボガドロの法則が成り立つため、
\[
\frac{P_1 V_1}{nT_1} = \frac{P_3 V_3}{nT_2}
\]
すなわち、
\[
\frac{PV}{nT}=一定=R
\]
圧力、物質量、温度について
圧力は単位面積当たりにかかる力と定義されます。ある面積\(S\)の板を、力\(F\)で押しているとすると、圧力\(P\)は次のように定義されます。単位はパスカル[Pa]です。
\[P=\frac{F}{S}\]
\(n\)は気体の物質量を意味しますが、物質量とは、6.02214076 ×1023個の粒子を1つの要素として数えたときの数で、単位はモル[mol] です。6.02214076 ×1023 mol−1はアボガドロ定数と呼ばれ、\(N_\mathrm A\)と書かれます。 例えば、\(2N_\mathrm A\)個の粒子は2 molです。
では、温度とは何なのでしょうか。日差しに当たるとポカポカして暖かいですが、暖かいとは、温度が適度に高いことを意味する形容詞です。同様に、寒いとは、温度が低いことを意味する形容詞です。
私たちは、普段から「温度」を感じています。皆さんは、温度とは何かと聞かれたら、どのように説明するでしょうか。
これは少し難しい話なのですが、現代において、温度とは分子運動の尺度と解釈されています。
理想気体の状態方程式を見ると、\(n\)一定で\(T\)が大きくなると\(P\)または\(V\)が大きくなります。分子運動が激しくなれば単位面積あたりに作用する力は強くなるし、体積も広がる方向に変化することが分かります。詳しくは「ボルツマン分布」などで説明されます。
また、科学(化学)では一般に熱力学温度(絶対温度)と呼ばれる温度を使い、単位はケルビン[K]を用います。普段から私たちが使っている摂氏温度\(T_\mathrm c [^\circ \mathrm C]\)と熱力学温度\(T_\mathrm k [\mathrm K]\)とは次のような関係があります。
\[
T_\mathrm c = T_\mathrm k – 273.15
\]
また、摂氏温度に負の数は存在しますが、熱力学温度には0または正の整数しか存在しません。
実在気体とは
理想気体以外の気体を実在気体と言います。実在する気体は理想気体ではないため、この名前がついたのでしょう。
実在気体を完璧に記述する方程式は今のところありませんが、多数の方程式が提案されています。その中でも、ファンデルワールスの状態方程式は、実在気体の本質を良くとらえているとされ、有名です。
\[
\left(
P+a\frac{1}{{\bar{V}}^2}
\right)
(\bar V+b)=RT
\]
実在気体において、理想気体とどれだけ乖離しているかを表す指標として、圧縮因子\(z\)があります。
\[
z:=\frac{P\overline{V}}{RT}
\]
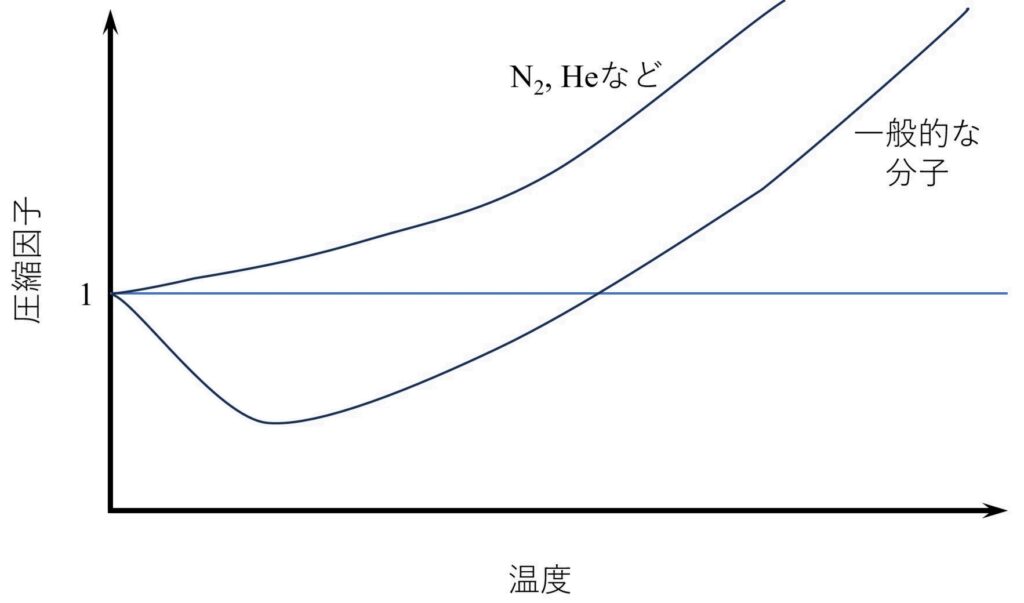
理想気体の場合、\(z=1\)となります。また、一般にT [K]=0からある一定温度までは\(z<1\)、それ以降は\(z>1\)となります。
温度が低い時、分子の運動は穏やかなため、分子間力が無視できず、理想気体よりも体積が小さくなります。そのため、\(z<1\)となります。
温度が高い時、分子の運動が激しいため、分子間力が無視できます。すると今度は分子の反発力が相対的に大きくなり、理想気体に比べて体積が大きくなります。そのため、\(z>1\)となります。
実在気体について詳しく知りたい方へ
ここでは実在気体について軽く触れるにとどまりました。もっと詳しく知りたい方はこちらをご覧ください。
