不飽和度(水素不足指数)とは
不飽和度(水素不足指数)とは、二重結合や環構造などの化合物がどの程度不飽和かを表す指数です。二重結合が\(I\)個、三重結合が\(m\)個、環構造が\(n\)個ある有機化合物の不飽和度は\(l+2m+n\)で表します。
つまり、多重結合や環の形成で、飽和な化合物に比べて水素を2\(I\)個だけ少ないとき、不飽和度は\(I\)になります。
二重結合が1つある有機化合物は水素分子1つで飽和化合物になり、三重結合を持つ有機化合物は水素分子2つで飽和化合物になります。
さらに、環構造は、任意の炭素-炭素結合を切って切り口に水素原子を1つずつ(水素分子を1つ)付加させることで飽和化合物になります。
このように不飽和度とは飽和化合物と比べてどれくらい水素分子が不足しているのかを表しているとも言えます。このようなことから、水素不足指数とも呼ばれます。
分子式がCaHbNcOdである有機化合物の不飽和度\(I\)は、次の式で表せます。
\[
I=\frac{2a-b+c+2}{2}
\]
上の式からわかるように、酸素原子の数は不飽和度に関係しません。
そして、\(I\)のとき、その化合物は飽和であるといい、\(I=1, 2, 3, \cdots\)のとき、その「鎖状」化合物は不飽和であるといいます。
(環構造は不飽和度が1以上ですが、二重結合や三重結合といった不飽和結合をもっていなければそれは飽和化合物です。)
不飽和度の導出(枝分かれのない場合)
では、なぜ不飽和度は分子式を見ただけでわかるのでしょうか。それは、有機化合物が共有結合で成り立っていることに由来します。
炭素は腕を4本もち、窒素、酸素、水素はそれぞれ3本、2本、1本です。いま、枝分かれのない飽和な有機化合物を考えます。
両端以外の原子がもつ腕のうち2つは鎖状を形成するために使わなければならないため、下の図からわかるように、炭素原子は2つの水素原子と結合でき、窒素原子は1つの水素原子と結合できます。酸素は水素と結合できません。
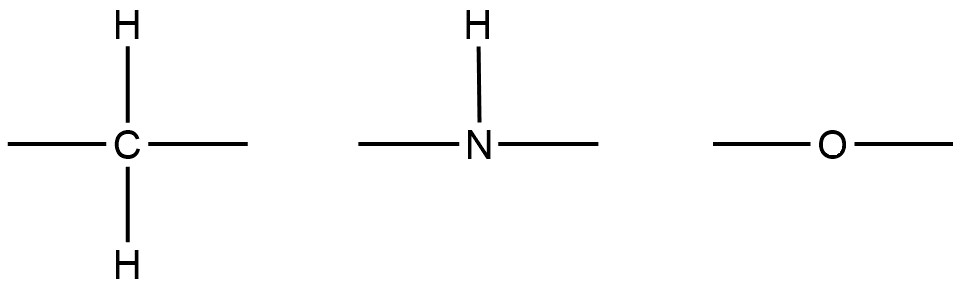
ここで、化合物の端の部分を見てみます。端の原子は鎖状を作るために必要な腕は1つだけなので、端ではない部分に比べて水素原子を1つ多く結合できます。
それが両端に存在するので、結果として水素の数は2つ多いことになります。
さて、下準備が終わりました。ここから不飽和度の式を導出します。
上の議論から、両端の水素2つを除くと、\(a\)個の炭素は\(2a\)個、\(c\)個の窒素は\(c\)個、\(d\)個の酸素は0個の水素原子を持つため、これらの和、\(2a+c\)に両端の水素2個を足した\(2a+c+2\)個の水素を持つときは不飽和度が0であることがわかりました。
ここから水素原子の数を2個引いた時、つまり水素原子が\(2a+c+2-2\)個の時、不飽和度は1です。同様にして、不飽和度が\(I\)の時、水素原子の数bは次の式を満たします。
\[b=2a+c+2-2I\]
よって、Iは次のように表せます。
\[
I=\frac{2a-b+c+2}{2}
\tag1
\]
このようにして、不飽和度の式を導出することができます。
不飽和度の導出(枝分かれのある場合)
枝分かれがある時は、端以外の原子に付加している水素を取り除き、そこに別の直鎖を付加したと考えます。
すると、枝分かれを作るために水素1つを取り除き、枝分かれができたことで新たに端が1つできたことから水素が1個多く付加されるため、結果的に枝分かれがない場合と同じ式が適用できます。
数学的に説明するなら、次のようなやり方が考えられます。
まず、枝分かれがない場合の導出ができているので、枝分かれをどうにかしてなくしてみます。ということで、大胆に枝分かれを切ってしまいましょう。切り口には水素を付加しておきます。
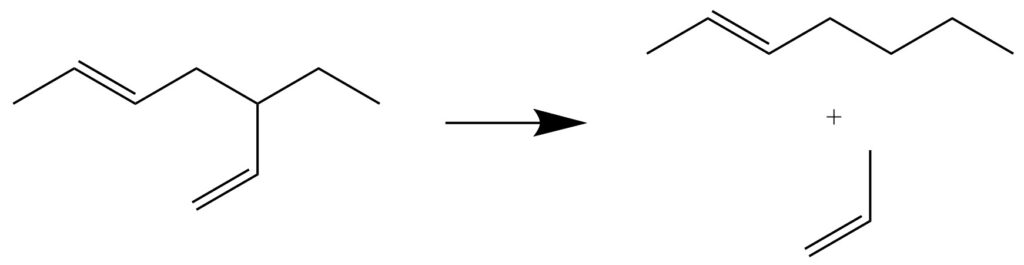
ここで、ひとつの有機化合物が複数に分裂しましたが、例えば2つに分かれたとき、この二つがそれぞれひとつずつ二重結合を持っているとき、元の有機化合物の不飽和度は1+1=2になります。
このように、枝分かれのある有機化合物の不飽和度は、枝分かれを切って新たにできた有機化合物の不飽和度の和になります。
いま、枝分かれがn個ある、分子式がCaHbNcOdで表される有機化合物の不飽和度Iを求めます。
この化合物の枝を切り、切り口に水素を付加させると、新たにn+1個の直鎖状有機化合物ができます。
そしてこれらの化合物に、O1, O2,⋅⋅⋅,On, On+1と名前を付けます。この時、kを1からn+1の任意の整数として、Okの分子式を CakHbkNckOdkとします。このことから、次の式が成り立ちます。
\[a=\sum_{k=1}^{n+1} a_k\]
\[b=\sum_{k=1}^{n+1} b_k\]
\[d=\sum_{k=1}^{n+1} d_k\]
なお、枝分かれを切った際に切り口に水素原子を合計2n個つけたため、bについての式だけ注意が必要です。
\[b=\sum_{k=1}^{n+1} b_k-2n\]
また、Okの不飽和度\(I_\mathrm{k}\)は、(1)式より次のようになります。
\[I_k=\frac{2a_k-b_k+c_k+2}{2}\]
よって、もとの有機化合物の不飽和度Iは、
\[
\begin{align}
I&=\sum_{k=1}^{n+1} I_k \\
&=\sum_{k=1}^{n+1} \frac{2a_k-b_k+c_k+2}{2} \\
&=\frac{2a-(b+2n)+c+2(n+1)}{2} \\
&=\frac{2a-b+c+2}{2}
\end{align}
\]
これで、枝分かれがある場合の不飽和度も、結局同じ形の式で表現できることがわかりました。
C, H, N, O以外の原子がある場合
C,H,N,O以外の原子がある場合は不飽和度をどのように考えればよいかは、今までの導出を理解していれば簡単な話です。
たとえば、リンPをふくむ場合、Pの腕の数は3本であるから、N原子と同じ扱いをしてよいのです。よって、分子式がCaHbNcOdPeである有機化合物の不飽和度\(I\)は、次の式で表せます。
\[I=\frac{2a-b+(c+e)+2}{2}\]
同様にして、他の元素をふくむときも、不飽和度の式を少し改造すれば良いということです。
