連続の概念は図形的に理解している方は多いかと思いますが、厳密な定義はご存じでしょうか？当記事では、連続の厳密な定義について解説します。
連続の意味と厳密な定義
次の\(f(x)\)、\(g(x)\)、\(h(x)\)について、\(x \to 2\)の極限はどうなるでしょうか。
\[
f(x)=
\begin{cases}
2x+1 & (x \neq 2)\\
6 & (x=2)
\end{cases} \\
\ \\
g(x)= \frac{(2x+1)(x-2)}{x-2}\\
\ \\
h(x)=2x+1\\
\]
答えは、すべての関数について\(5\)です。計算過程がすべて同じなことはすぐにわかるかと思います。
極限についてはこちらをご覧ください。
\(f(x)\)、\(g(x)\)、\(h(x)\)の極限はどちらとも同じですが、グラフの見てくれは違います。
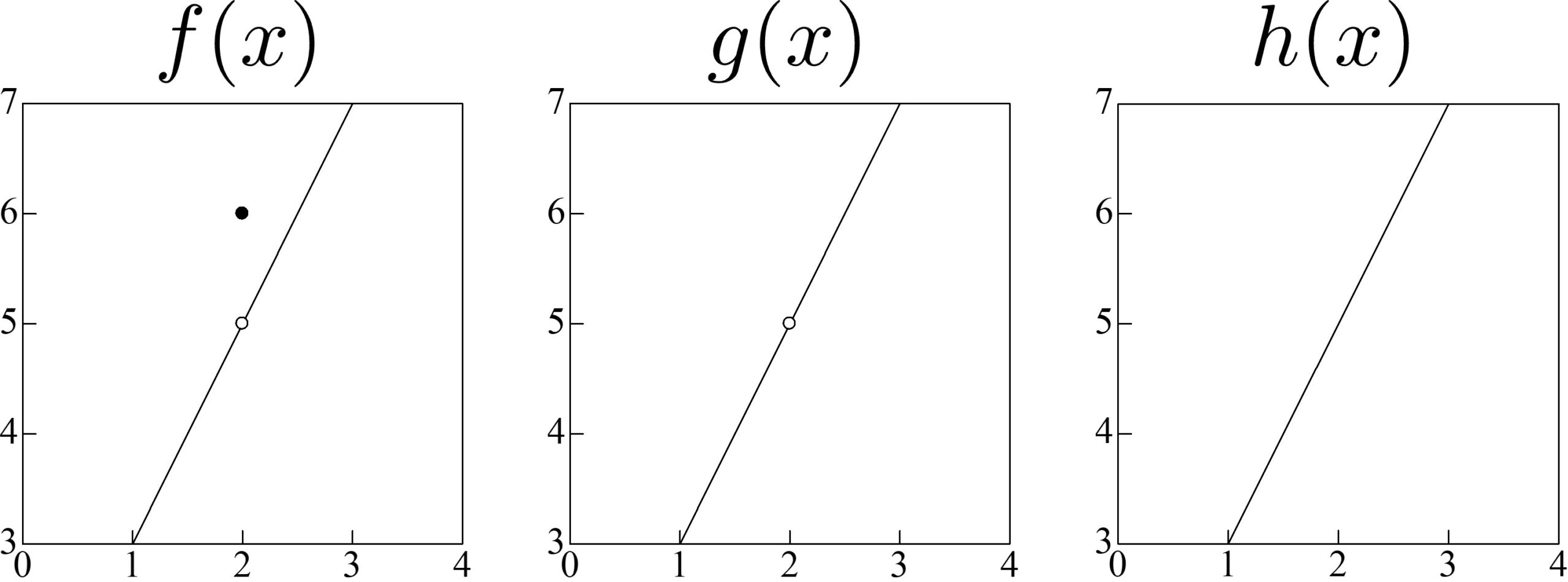
まず\(f(x)\)を見ると、\((x, f(2))\)の点だけ\(y=2x+1\)から上にずれています。
\(g(x)\)については、\((x, g(2))\)の点で定義されていません。そのせいで\(y=2x+1\)が途中で切れているように見えます。
そして\(h(x)\)は、点\((2, h(2))\)とその前後の値が連続につながっています。
\(f(x)\)や\(g(x)\)が連続につながっていないと感じるのは、\(x=2\)での挙動がその前後の流れに反するからでしょう。
\(x=2\)に限りなく近づけていくとき、\(f(x)\)や\(g(x)\)は5に近づきそうに見えるのに、実際はそうではないので、不連続に感じるのです。
そこで、連続を次のように定義します。
関数\(f\)が定義域内の数\(a\)において、
\[
\lim_{x\to a}f(x)=f(a)
\]
であるとき、\(f\)は\(a\)で連続であるという。
また、\(f\)が定義域内のすべての数で連続である時、関数\(f\)は連続であると表現する。
加えて、\(f\)が連続でないとき、\(f\)は不連続であるという。
\[
\lim_{x\to a^+}f(x)=f(a)
\]
であるとき、\(f\)は\(a\)で右連続であるという。
同様に、
\[
\lim_{x\to a^-}f(x)=f(a)
\]
であるとき、\(f\)は\(a\)で左連続であるという。
不連続点の種類
除去可能な不連続点
先ほどの図1に示した\(f(x)\)や\(g(x)\)のように、不連続な点だけ定義しなおせば連続な関数になるとき、これを除去可能な不連続点と呼びます。
関数\(f\)の定義域内で、\(x \to a\)における\(f\)の右極限と左極限が定義されており、これが共に有限値\(L\)であるが、\(L \neq f(a)\)であるとき、点\((a, f(a))\)を除去可能な不連続点という。
跳躍不連続点
\(f(x)=[x]\)を考えます。ただし、\([x]\)とは\(x\)以下最大の整数を意味します（これをガウス記号といいます）。
任意の整数\(m\)について、\(x = m \)のとき、\(f(m)=m\)ですが、右極限と左極限の値が互いに異なります。
\[
\begin{align}
\lim_{x \to m^-} f(x)&=m-1\\
\lim_{x \to m^+} f(x)&=m
\end{align}
\]
このように、右極限と左極限が違うために不連続点でグラフが「跳躍」しているとき、これを跳躍不連続点といいます。
関数\(f\)の定義域内で、\(x \to a\)における\(f\)の右極限と左極限が定義されており、これが異なる有限値をとるとき、点\((a, f(a))\)を跳躍不連続点という。
無限不連続点
ここまでで2つの不連続点を見てきました。
除去可能な不連続点では、右極限と左極限が有限値で等しく、
跳躍不連続点では、右極限と左極限が有限値で異なる。
とすれば、残りは右極限と左極限の少なくとも一方が有限値でない場合となります。
そこで、\(f(x)=1/x\)を考えます。
\(f(x) \to \infty \ (x \to 0)\)ですから、これは連続ではありませんし、かつ、極限が有限値ではないので、これは除去可能な不連続点でもなければ跳躍不連続点でもありません。
このように、「無限」が関与する不連続点を無限不連続点といいます。
関数\(f\)の定義域内で、\(x\to a\)における\(f\)の右極限と左極限のうち、少なくとも一方が有限値にならないとき、点\((a, f(a))\)を無限不連続点という。
なお、無限不連続点は真性不連続点とも呼ばれます。
連続な関数
最後に、馴染みのある連続関数を紹介します。
多項式、有理関数、べき乗根関数、指数関数、対数関数、三角関数は定義域で連続関数である。
連続関数\(y=f(x)\)について\(f(a)=b\)とし、逆関数\(x=f^{-1}(y)\)が存在するとき、\(f\)が\(a\)で連続であるならば、\(f^{-1}\)は\(b\)で連続である。
別の記事で紹介したように、べき関数指数関数、対数関数、三角関数は微分可能であるので、これらは連続です（微分可能ならば連続という定理はこちら）。
また、べき関数の線形結合からなる多項式や、多項式の商である有理関数も、分母が0になる点を除いて連続です（詳しくは極限の公式を参照）。
逆関数の連続性も微分可能性で証明したいところですが、当記事では逆関数が微分可能であることの証明で逆関数の連続性を仮定しているため、ここでは素直に定義から連続性を証明します。
逆関数が連続であることの証明
そもそも、関数\(f\)の逆関数\(f^{-1}\)とは、\(f{^-1}(f(x))=f(f^{-1}(x))x\)を満たすものをいいます。
ある数\(a, b ( a \neq b)\)に対して、\(f(a)=f(b)=A\)となると、\(f^{-1} (A) = a, b \)となるため、逆関数は存在しません。したがって、関数\(y=f(x)\)に対してその逆関数\(x=f^{-1}(y)\)が存在するなら、\(a \neq b \Longrightarrow f(a) \neq f(b) \)です。
連続関数\(y=f(x)\)に対してその逆関数\(x=f^{-1}(y)\)が存在するためには、関数\(f\)は単調増加関数または単調減少関数であることが必要十分です。まずはこれを証明しましょう。
相異なるある数\(x_1 ,x_3\)に対して、\(f(x_1) < f(x_3) \)とする。\(f\)が単調増加あるいは単調減少でなければ、\(x_1 ,x_3\)の間のある数\(x_2\)が存在して、\(f(x_2) < f(x_1) < f(x_3) \)または\(f(x_1) < f(x_3) < f(x_2) \)である。
(i)\(f(x_2) < f(x_1) < f(x_3) \)のとき、中間値の定理より、\(x_1, x_2\)の間にある数\(c_1\)が存在して、
\[
\begin{align}
N=f(c_1) && (f(x_2) < N < f(x_1))
\end{align}
\]
となるNが存在する。
また、\(x_2, x_3\)の間にある数\(c_2\)が存在して、
\[
\begin{align}
N = f(c_2) && (f(x_2) < N < f(x_1) < f(x_3))
\end{align}
\]
となるNが存在する。
よって、\(c_1 \neq c_2 \Longrightarrow f(c_1)=f(c_2)\)を満たすある数\(c_1, c_2\)が存在するため、\(f\)の逆関数は存在しない。
(ii)\(f(x_1) < f(x_3) < f(x_2) \)のとき、中間値の定理より、\(x_1, x_2\)の間にある数\(c_3\)が存在して、
\[
\begin{align}
N=f(c_3) && (f(x_1) < f(x_3) < N < f(x_2))
\end{align}
\]
となるNが存在する。
また、\(x_2, x_3\)の間にある数\(c_4\)が存在して、
\[
\begin{align}
N = f(c_4) && (f(x_3) < N < f(x_2))
\end{align}
\]
となるNが存在する。
よって、\(c_3 \neq c_4 \Longrightarrow f(c_3)=f(c_4)\)を満たすある数\(c_3, c_4\)が存在するため、\(f\)の逆関数は存在しない。
以上、(i)(ii)より、連続関数\(f\)に逆関数が存在するなら、\(f\)は単調増加または単調減少関数である。
逆に、\(f\)が単調増加または単調減少関数であるとき、相異なる任意の数\(x_1, x_2\)に対して、\(f(x_1) \neq f(x_2)\)であるから、これは逆関数をもつ。
それでは、逆関数の連続性を証明する。
関数\(y=f(x)\)が連続な単調増加関数であるとき、逆関数\(x=f^{-1}(y)\)が存在する。
ここで、\(y=f(x)\)は単調増加関数だから、任意の\(\varepsilon_2>0\)に対して定義域を閉区間\([a-\varepsilon_2, a+\varepsilon_2]\)とすると、その値域は\([f(\alpha-\varepsilon_2), f(a+\varepsilon_2)]\)である。したがって、 \(\delta_2=\min \{ f(a+\varepsilon_2)-b, b-f(a+\varepsilon_2) \} \)とすれば、
\[
|y-b| < \delta_2 \Longrightarrow |f^{-1}(y)-f^{-1}(b)| < \varepsilon_2
\]
は真である。
以上より、関数\(f(x)\)が\(x=a\)で連続かつ逆関数\(x=f^{-1}(y)\)をもつならば、逆関数は\(y=b\)で連続である。
\(f\)が単調減少関数の場合も同様に示すことができます。
ポイントは、定義域\([a,b]\)に対応する値域が、単調増加関数だと\([f(a), f(b)]\)で、単調減少関数だと\([f(b), f(a)]\)となってくれるところです。
次に、limと関数が交換できる場合を紹介します。
関数\(f(x)\)は\(b\)で連続、\(u=g(x)\)の値域は\(f(x)\)の定義域の部分集合であり、\(\displaystyle \lim_{x \to a} g(x)= b\)であるとする。このとき、
\[
\lim_{x \to a}f(g(x)) = f(b) =f(\lim_{x \to a}g(x)) \tag1
\]
また、\(f(x)\)は\(b\)で連続だから、
\[
\lim_{x \to a} f(u) = f(b) = \lim_{u \to b} f(u) \tag2
\]
定理1の証明を表示
[証明]
任意の\(\varepsilon_1 >0\)に対して、ある\(\delta_1 >0\)が存在して、
\[
0<|x-a|<\delta_1 \Longrightarrow |u-b|<\varepsilon_1 \tag{1.1}
\]
同様に、任意の\(\varepsilon_2 >0\)に対して、ある\(\delta_2 >0\)が存在して、
\[
0<|u-b|<\delta_2 \Longrightarrow |f(u)-f(b)|<\varepsilon_2 \tag{1.2}
\]
ここで、\(\varepsilon_1 = \delta_2\)としても(1.1)は成立する。
\(u \neq b\)なら\(|u-b|<\delta_2 \Longleftrightarrow 0<|u-b|<\delta_2\)なので、(1.1)(1.2)より、
\[
0<|x-a|<\delta_1 \Longrightarrow 0<|u-b|<\delta_2 \Longrightarrow |f(u)-f(b)|<\varepsilon_2
\]
\(u = b\)なら、任意の\(x\)で\(|f(u)-f(b)|<0\)より、
\[
0<|x-a|<\delta_1 \Longrightarrow |f(u)-f(b)|<\varepsilon_2
\]
以上より、
\[
\lim_{x \to a}f(g(x)) = f(b)
\]
(1)式はlimと極限が交換できるという性質を表しています。
(2)式は、\(x\)を\(a\)へ限りなく近づけたときに、\(u\)は\(b\)に限りなく近づくから、\( \displaystyle \lim_{x \to a} \)を\(\displaystyle \lim_{u \to b} \)と書き換えたくなりますが、そうしてもよいということを定理としてしっかりと主張しているということになります。
関数\(g\)は\(a\)で連続、関数\(f\)は\(b=g(a)\)で連続であるとする。このとき、合成関数\(f\circ g\)は\(a\)で連続である。すなわち、
\[
\lim_{x \to a}f(g(x))=f(g(a))
\]
補題1の証明を表示
定理1より、
\[
\lim_{x \to a}f(g(x))=f(g(a))
\]