微分の厳密な定義

極限を使って微分を定義し、重要な定理を導きます。

接線の引き方

微分学を発展させたうちの一人であるニュートンは、フェルマーやバローといった数学者が用いていた”接線“を求める方法に精通していたからこそ、微分学を定式化させることができたと言ったそうです。

では、接線の求める方法から微分に導入していこうと思います。

次のグラフに示すような接線を引く方法を考えます。

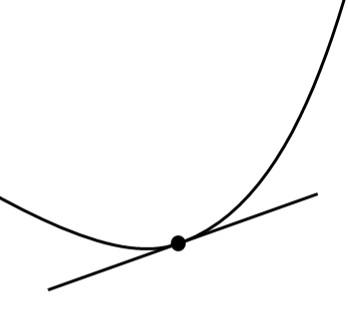
接線を求めたい点（黒点）とそこから少し離れた点（赤点）を結ぶ線を引きます。その後、赤点を黒点に近づけていくと、求めたい接線となりそうです。

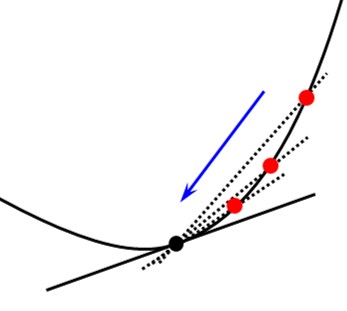
以上より、接線を次のように定義します。

微分係数・導関数

接線の傾きの定義式は、\(x=a\)における\(f(x)\)の変化率ともいえるでしょう。つまり、\(x=a\)における接線の傾きは、\(x=a\)の瞬間、\(f(x)\)がどれくらいの速さで変化しているかを表しているように感じられます。

例えば、車に乗ってスタート地点から時間\(t\)が経過した時に\(x=t^2\)の場所にいるような状況を考えます。

このとき、車はどれくらいの速さで走っているのでしょうか？\(x=t^2\)なので、徐々に速くなっている、つまり刻々と速さが変っていることがわかります。

速さが一定なら、(距離)/(時間)を計算すれば、これがすべての地点の速さになったのですが、今回の場合はこれだとうまくいきません。

ひとまず、(距離)/(時間)の形を作ってみましょう。\(t=t_1, t_2 \)を用いて、

\[
\frac{{t_2}^2-{t_1}^2}{t_2-t_1}
\]

これをどうにかして速さにするにはどうすればよいでしょうか。

先ほど、\(x=a\)における接線の傾きは、\(x=a\)の瞬間、\(f(x)\)がどれくらいの速さで変化しているかを表しているように感じられると説明しました。

そこで、\(t_2\)を\(t_1\)に限りなく近づけたらどうでしょうか。こうすれば\(\t_1)における速さと言えるのではないでしょうか。

\[
\lim_{t \to t_1}\frac{{t}^2-{t_1}^2}{t-t_1}
\]

なお、上式では\(t_2\)を\(t\)でおきかえました。

このように、接線の傾きに出てくる極限は何かと便利なので、特別な名前がついています。

微分係数はもう一つ重要な表現方法があります。

\(x=a+h\)とおくと、

\[
|x-a|<\delta \Longleftrightarrow |h-0|<\delta
\]

よって、次のことがいえます。

さらに、\(x=a\)に限らず任意の\(x\)で微分係数を考えたいこともあります。その場合は、導関数という別の名前がついています。

導関数や微分係数の表記にはいくつか種類があります。

\[y=f(x) \Longrightarrow f'(x)=y’=\frac{dy}{dx}=\frac{df}{dx}=\frac{d}{dx}f(x)\]

\[f'(a)= \left. \frac{dy}{dx} \right|_{x=a} \]

微分に関する重要な定理・公式

証明はこちら

\[
\begin{align}
\lim_{x \to a}f(x)
&=\lim_{x \to a}(f(x)-f(a)+f(a)) \\
&=\lim_{x \to a} \left( \frac{f(x)-f(a)}{x-a}\cdot(x-a)+f(a) \right) \\
&=f'(a) \cdot 0 + \lim_{x \to a} f(a) \\
&=f(a)
\end{align}
\]

定義通りに連続性を証明することが面倒な関数は多く存在します。その際にこの定理が威力を発揮します。しかし、関数が連続だからと言って、必ずしも微分可能ではありません。例えば、\(y=|x|\)は\(x=0\)で連続ですが微分不可能です。

続いて、中間値の定理です。

証明は難易度が高いため、割愛します。

何かと面白い定理の証明に使われます。