定積分
三角形や四角形の面積は簡単に求められますが、複雑な形の図形の面積はどうやって求めたらよいのでしょうか？
\(x\)軸と\(y=f(x)\)、\(x=a\)、\(x=b\)で囲まれた面積\(S\)の求め方を考えてみます。
面積の基本は四角形です。三角形の面積も、四角形の面積を2で割って求めるのでした。
そこで、このように四角形で埋めてみましょう。
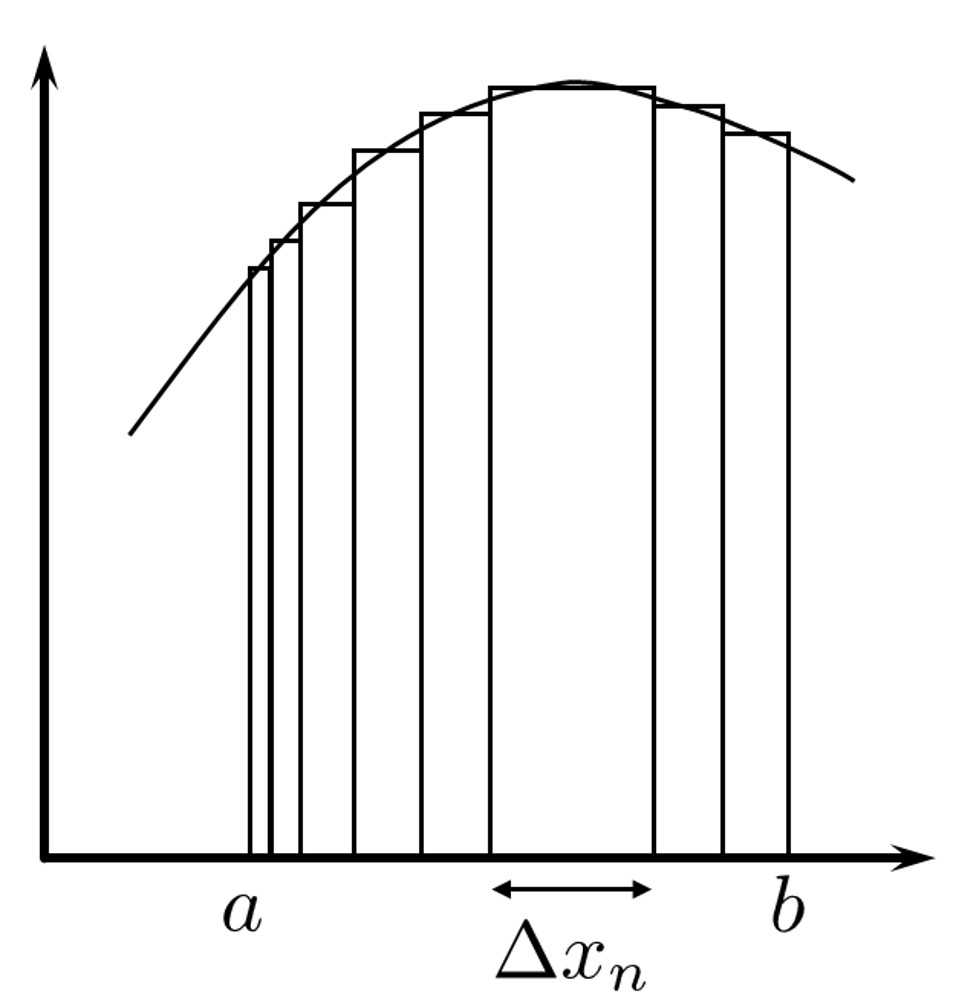
この四角形を限りなく小さくしたら面積がわかるのではないか、という発想です。
この四角形を数学的に扱うために、以下のように定めます。
閉区間\([a, b]\)を\(n\)個の区間に分けます。\(a=x_0 < x_1 < \cdots < x_{n-1} < x_n = b\)とし、\(\Delta x_i = x_i-x_{i-1} (i=1, 2, \cdots , n)\)を定義します。この\(\Delta x_i\)を四角形の横幅としましょう。
四角形の横幅すなわち\(\Delta x_n\)は均等でなくてもよいでしょう。なぜなら、面積を求めるにあたって、\(f'(x)=0\)付近では\(\Delta x_n\)を大きめにとっても良い近似になりそうですが、\(f'(x)\)が\(0\)からはなれた場所だと\(\Delta x_n\)は小さく取らないといけなそうだからです。
また、代表点なる点\({x_i}^* (x_{i-1} \leq {x_i}^* \leq x_i)\)をとり、これを四角形の横幅\(\Delta x_i\)に対する縦の長さとします。
そして、\(\displaystyle S_n = \sum_{k=1}^n f({x_i}^*) \Delta x_i\)を\(S\)の近似値としましょう。
さて、\(n\)を大きくしたら、\(S_n\)は\(S\)にいくらでも近づくと考えられます。
これは、数列の極限の定義そのものです（URLの記事は関数の極限についてのものですが、数列の極限も同様に考えます）。すなわち、
\[
\lim_{n \to \infty} S_n = S
\]
言い換えると、任意の数\(\varepsilon\)に対してある数\(N\)が存在して、次の命題が真であるということです。
\[
n>N \Longrightarrow |S_n -S| < \varepsilon
\]
かくして、面積を次のように定義します。
\(f\)を閉区間\([a, b]\)で定義された関数とする。\(a=x_0 < x_1 < \cdots < x_{n-1} < x_n = b\)とし、\(\Delta x_n = x_n -x_{n-1}\)を定義する。いま、\(n\)個の代表点\( {x_n}^* (x_{n-1} \leq {x_n}^* \leq x_n)\)をとり、極限
\[
\lim_{n \to \infty} \sum_{k=1}^n {f({x_n}^*)\Delta x_n}
\]
が存在して、代表点の取り方によらず、すべての極限値が等しいとき、この極限を
\[
\int_a^b f(x)dx
\]
と表し、\(a\)から\(b\)までの\(f\)の定積分という。この極限が存在する関数を\([a, b]\)で積分可能な関数という。
定積分の重要な定理
閉区間\([a, b]\)で関数\(f\)が連続または跳躍不連続点が高々有限個しかないなら、\(f\)は閉区間\([a, b]\)で積分可能である。
証明は割愛します。関数列の極限について学べば証明できます。そこまで難しくないです。
\[
\begin{align}
\int_a^b c \ dx = c(b-a) && (c = \text{const.}) \tag1
\end{align}
\]
\[
\begin{align}
\int_a^b (f(x) \pm g(x)) dx = \int_a^b f(x) dx \pm \int_a^b g(x) dx && (\text{複合同順}) \tag2
\end{align}
\]
\[
\begin{align}
\int_a^b cf(x) dx = c\int_a^b f(x) dx && (c = \text{const.}) \tag3
\end{align}
\]
\[
\int_a^c f(x)dx = \int_a^b f(x)dx + \int_b^c f(x)dx \tag4
\]
(1)式の証明を表示
代表点をどこにとっても\(f({x_n}^*)=c\)である。任意の\(n\)について\(S_n=c(b-a)\)だから、
\[
\int_a^b c \ dx = c(b-a)
\]
(2)式の証明を表示
\[
\begin{align}
\int_a^b (f(x) \pm g(x))dx &= \lim_{n \to \infty} \sum_{k=1}^n {(f({x_n}^*) \pm g({x_n}^*)) \Delta x_n} \\
& = \lim_{n \to \infty} \sum_{k=1}^n (f({x_n}^*) \Delta x_n \pm g({x_n}^*)\Delta x_n )\\
& = \lim_{n \to \infty} \sum_{k=1}^n f({x_n}^*) \Delta x_n \pm \lim_{n \to \infty} \sum_{k=1}^n g({x_n}^*)\Delta x_n \\
& = \int_a^b f(x) dx \pm \int_a^b g(x) dx
\end{align}
\]
(3)式の証明を表示
\[
\begin{align}\int_a^b cf(x) dx &= \lim_{n \to \infty} \sum_{k=1}^n cf({x_n}^*) \Delta x_n \\
&=\lim_{n \to \infty} c\sum_{k=1}^n f({x_n}^*) \Delta x_n\\
&=c\int_a^b f(x) dx
\end{align}
\]
(4)式が直感的に正しいことはすぐにわかるかと思いますが、証明は難しいです。
閉区間\([a, b]\)内の\(x\)について、
- \(f(x) \geq 0\)ならば、
\[
\int_a^b f(x)dx \geq 0 \tag5
\] - \(f(x) \leq g(x)\)ならば、
\[
\int_a^b f(x)dx \leq \int_a^b g(x)dx \tag6
\] - 定数\(m, M\)に対して\(m \leq f(x) \leq M\)ならば、
\[
m(b-a) \leq \int_a^b f(x)dx \leq M(b-a) \tag7
\]
(5)式の証明を表示
\(f(x)\geq0\)より、任意の\(i=0, 1, \cdots, n\)について、\(S_i\geq0\)である。
任意の\(\varepsilon>0\)に対して、ある\(N>0\)が存在し、
\[
n>N \Longrightarrow |S_n-S| < \varepsilon
\]
ここで、\(S<0\)と仮定すると、\(S_n\geq0\)より、\(S_n -S \geq -S > 0\)だから、
\[
\begin{align}
\begin{cases}
-\varepsilon < S_n -S < \varepsilon \\
0 < S_n-S
\end{cases}
\Longrightarrow 0 < S_n-S < \varepsilon \Longleftrightarrow S < S_n < S + \varepsilon
\end{align}
\]
しかし、\(\varepsilon \leq -S \Longleftrightarrow S + \varepsilon \leq 0 \)となるような\(\varepsilon\)を選ぶと\(S_n<0\)となるため、矛盾。
したがって、背理法より\(S \geq 0\)、すなわち、
\[
\int_a^bf(x)dx \geq 0
\]
(6)式の証明を表示
(5)式より、
\[
\begin{align}
f(x) \leq g(x) \Longleftrightarrow f(x) -g(x) \leq 0 &\Longrightarrow \int_a^b f(x)dx -\int_a^b g(x)dx \leq 0\\
&\Longleftrightarrow \int_a^b f(x)dx \leq \int_a^b g(x)dx
\end{align}
\]
(7)式の証明を表示
(1), (6)式より、
\[
\begin{align}
m \leq f(x) \leq M &\Longrightarrow \int_a^b mdx \leq \int_a^b f(x)dx \leq \int_a^b Mdx \\
&\Longrightarrow m(b-a) \leq \int_a^b f(x)dx \leq M(b-a)
\end{align}
\]
不定積分
関数\(f\)の不定積分とは、\(f\)の任意の原始関数です。
関数\(f\)の不定積分\(F\)を、次のように表す。
\[
F(x) = \int f(x)dx
\]
例えば、
\[
\begin{align}
\int x^2dx = \frac{x^3}{3} + C && (C=\text{const.})
\end{align}
\]
であり\(C\)を積分定数といいます。
置換積分
置換積分は、合成関数を積分するときに便利な方法です。
\(u=g(x)\)は値域が閉区間\([a, b]\)で、それに対応する定義域で微分可能な関数であり、関数\(f(u)\)は閉区間\([a, b]\)で連続な関数とすると、\(f(g(x))g'(x)\)は積分可能で、
\[
\int f(g(x))g'(x) \ dx = \int f(u) \ du
\]
\[
\int_a^b f(g(x))g'(x) \ dx = \int_{g(a)}^{g(b)} f(u) \ du
\]
定理4の証明
不定積分は合成関数の微分公式から導かれる。
定積分については、\(F\)を\(f\)の原始関数とすると、微分積分学の基本定理より、
\[
\begin{align}
\int_a^b f(g(x))g'(x) \ dx &= \Bigl[ F(g(x)) \Bigr]_a^b \\
&= \Bigl[ F(u) \Bigr]_{g(a)}^{g(b)} \\
&= \int_{g(a)}^{g(b)} f(u) \ du
\end{align}
\]
部分積分
部分積分は、関数の積からなる関数を積分するときに威力を発揮する方法です。
\(f\)と\(g\)が閉区間\([a,b]\)で微分可能ならば、\(f(x) g'(x)\)は積分可能で、
\[
\int f(x) g'(x) dx = f(x)g(x) -\int f'(x)g(x) dx
\]
\[
\int_a^b f(x) g'(x) dx = \biggl[ f(x)g(x) \biggr]_a^b -\int_a^b f'(x)g(x) dx
\]
定理5の証明
積の微分公式より、
\[
f(x)g'(x)= \frac{d}{dx}f(x)g(x) -f'(x)g(x)
\]
\[
\Longleftrightarrow \int f(x) g'(x) dx = f(x)g(x) + C -\int f'(x)g(x) dx
\]
積分定数Cを\(\int f'(x)g(x) dx\)のそれに含めると、
\[
\int f(x) g'(x) dx = f(x)g(x) -\int f'(x)g(x) dx
\]