ラジカル重合は、主にビニル化合物の重合方法として最も一般的に用いられます。
本記事では、ラジカル反応の素反応(開始反応、生長反応、停止反応、連鎖移動反応)と反応速度論について解説します。
ラジカル重合の素反応
ラジカル重合は、ラジカルを用いた重合のことです。ラジカル重合は以下の4つの素反応からなります。
- 開始反応(Initiation)
- 生長反応(Propagation)
- 停止反応(Termination)
- 連鎖移動反応(Chain transfer)
いま、開始剤を\(\mathrm I_2\)、モノマーを\(\mathrm M\)、ポリマーを\(\mathrm P\)、ポリマーラジカルを\(P_\mathrm n \cdot\)、モノマーを\(\mathrm {XY}\)、溶媒、開始剤などの連鎖移動剤とします。開始剤とは何か、といった詳しいことは後述します。
反応速度定数\(k\)、反応速度\(R\)をそれぞれ添え字をつけて以下の式に示すようにおくと、各素反応は以下のように記述することができます。
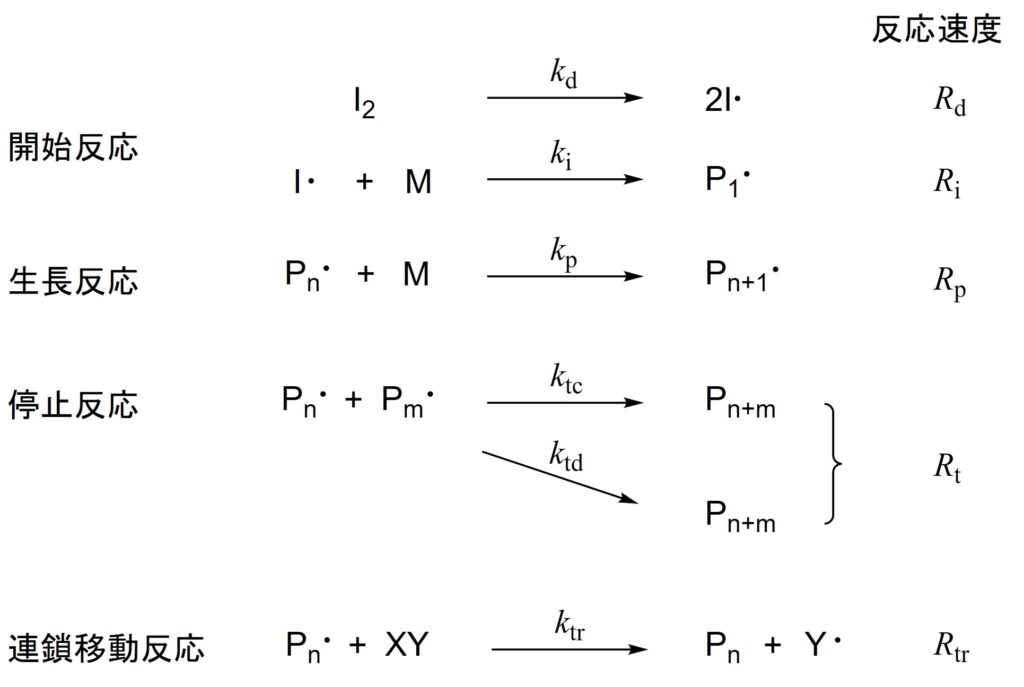
開始反応
開始反応とは、重合を開始するための反応です。
開始剤と呼ばれる、熱や光によって反応性の高い化学種(ラジカル重合の場合は開始ラジカルという)を生成する化合物をモノマーの入った系に投入し、開始ラジカルがモノマーと反応することによって重合のもとになる化学種(生長ラジカル)ができます。
代表的な開始剤として、過酸化ベンゾイル(BPO)とアゾビスイソブチロニトリル(AIBN、アイビンと読む)があります。
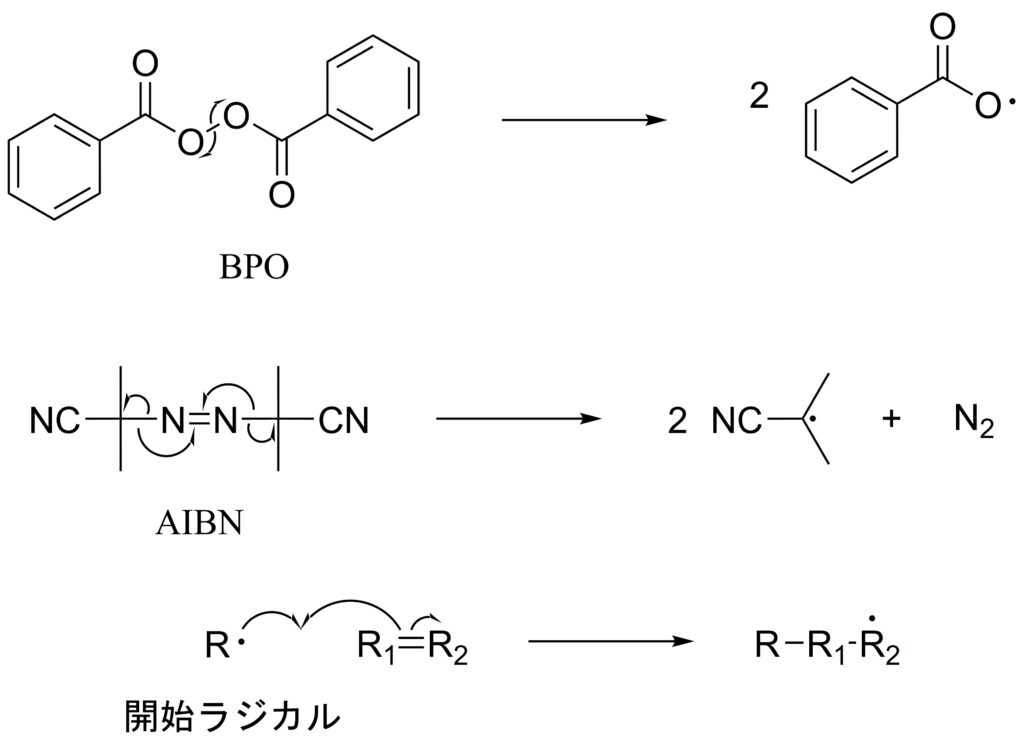
O−O結合やC=N結合はC−C結合やC−H結合の半分程度であることから、100 ℃程度の加熱でホモリシスを起こし、開始剤として機能します。
なお、ラジカルは級数の大きい方が安定であるため、R1にラジカルができるか、あるいはR2にできるかは官能基の種類に左右されます。
また、開始剤効率\(f\)と呼ばれる、開始ラジカルがモノマーに付加して生長ラジカルになる割合を表す値があります。
BPOの\(f\)は0.9−1.0、AIBNの\(f\)は0.5−0.7くらいです。
この差は、ホモリシス後の副反応が関係しています。BPOに関しては1 %未満の確率で脱炭酸が起こりますが、AIBNに関しては多くの副反応が比較的起こるため、\(f\)は小さくなります。
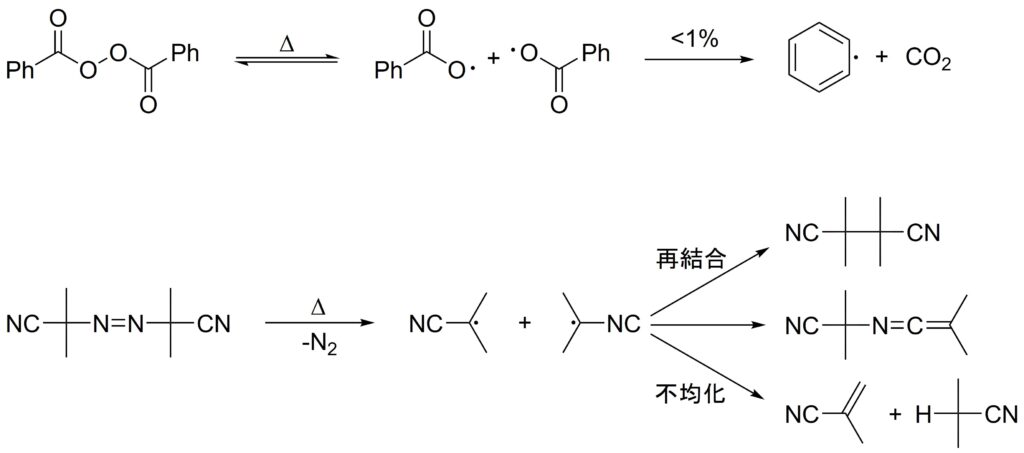
なお、一般に\(\mathrm I_2\)が開裂する反応は遅く律速段階であるため、開始ラジカルがモノマーに攻撃して生長ラジカルを生成する反応の反応速度は開始ラジカルの生成反応速度に大きく影響を受けます。詳しくはラジカル重合の反応速度論で後述します。
生長反応
開始反応によって生長ラジカルが生成したら、今度は生長ラジカルがモノマーの二重結合へ付加し、構成単位がひとつ増えた新たなラジカルを形成し、これが何度も反応することで分子鎖の長い高分子になります。これを生長反応といいます。
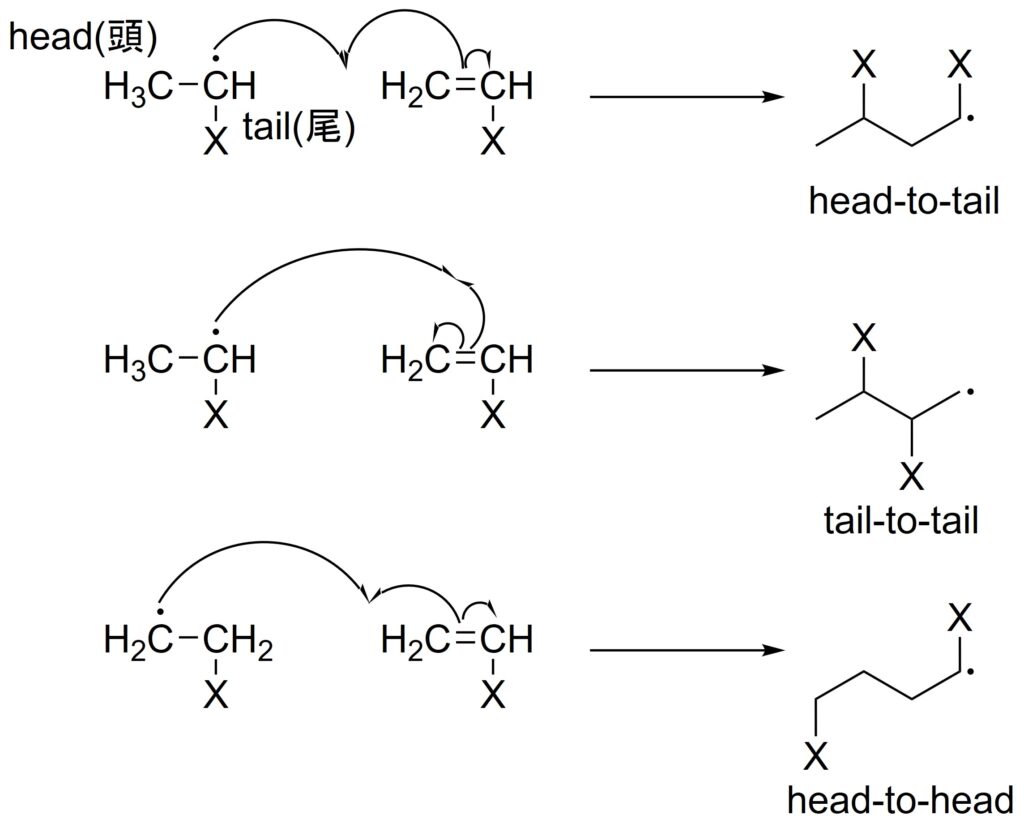
生長反応では、考え得る構造が3パターンあります。
いま、α炭素をhead(頭)、β炭素をtail(尾)と呼ぶと、headとtailが結合したhead-to-tail構造、tailとtailが結合したtail-to-tail構造、headとheadが結合したhead-to-head構造が考えられます。
しかし、殆どの系においてhead-to-tail構造の高分子が生成します。
これは、級数の大きなラジカルが安定であることに由来します。
tailにラジカルが生成するように反応すると、級数が最も高くなります。
そのため、tailのラジカルがheadと結合することによって再びtailにラジカルが生成する反応が優位に進み、head-to-tail構造が主に得られます。
ちなみに、置換基のXがしっぽに見えることが、headとtailの名前の由来です。
停止反応
停止反応とは生長末端のラジカル同士が反応することで重合反応が停止する反応です。停止反応には、再結合反応と不均化反応があります。
再結合反応とは、ラジカル同士が電子を出し合って再び共有結合を作る反応です。
不均化反応とは、一つの化学種が酸化剤と還元剤の両方の役割を果たす反応です。
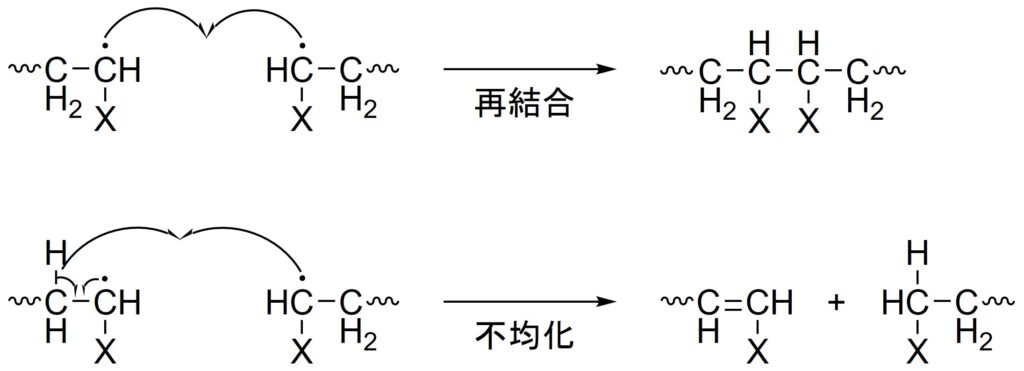
再結合と不均化の起こる割合は主にモノマーの種類によって決まります。
例えば、スチレンはほぼ100 %の割合で再結合が起こりますが、メタクリル酸メチルは約65 %の割合で不均化を起こします。
一般に生長反応に比べ停止反応の反応速度定数はずっと大きいため、停止反応が優先して起こります。このようなことから、ラジカル重合では高分子量のポリマーを生成しにくいです。
連鎖移動反応
生長ラジカルが、反応系中の様々な化学種に移動し、移動したラジカルから再び重合が始まる反応を連鎖移動反応といいます。
このため、反応系中のラジカル濃度は変わらず、重合速度は低下しませんが、生長末端のラジカルが奪われるため、その高分子の重合は停止し、分子量は小さくなります。
また、連鎖移動反応によって生成したラジカルも重合を開始させることが一般的です。
例として、四塩化炭素(溶媒)下でのスチレンのラジカル重合における連鎖移動反応を示します。
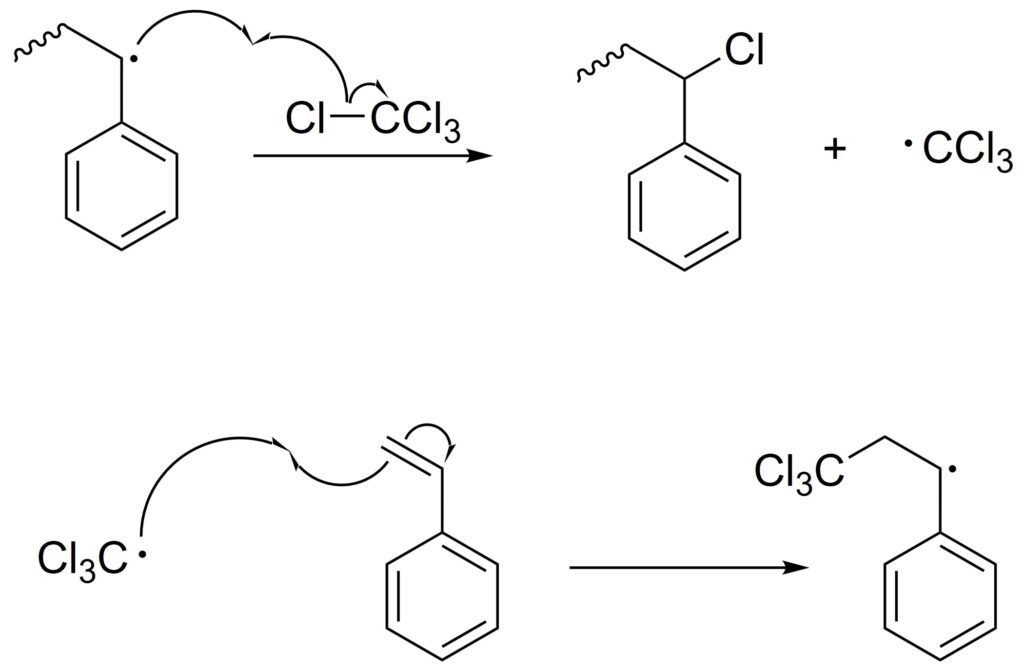
ラジカル重合の反応速度論
ラジカル重合の反応速度について考えます。以下に再掲する図1に示した反応速度定数と反応速度の表記を再度ご確認ください。

計算の簡略化のため、次の4つの仮定を置きます。
- 生成ラジカルの反応性は重合度に依らない。
- 生長ラジカルの分子量は十分に大きく、モノマーは成長反応によってのみ消失する。
- 生長ラジカルの濃度は一定、つまり生長ラジカルの生成速度と消失速度が等しい(定常状態近似)。
- 連鎖移動反応が起こっても開始反応が速ければ、重合速度は低下しない。
それでは、具体的に反応速度を記述します。
\[
R_\mathrm{d}=2k_\mathrm{d}[\mathrm{I_2}]
\tag1
\]
\[
R_\mathrm{i}=2k_\mathrm{d}f[\mathrm{I_2}]
\tag2
\]
\[
R_\mathrm{p}=k_\mathrm{p}[\mathrm{P_n\cdot}][\mathrm{M}]
\tag3
\]
(2)の\(R_\mathrm i\)に関しては、\(R_\mathrm d\)が律速であることから\(R_\mathrm i=R_\mathrm d\)としたいところですが、(1)式の\( [ \mathrm I_2 ] \)を実際に開始剤として反応するモノマー濃度\(f [ \mathrm I_2 ] \)に置き換えることで(2)式を表現します。
仮定2より、モノマーは生長反応のみで消費されることから、重合速度はモノマーの消費速度と等しくなります。よって、\( [\mathrm M] \)は次式のように表せます。
\[
R_\mathrm{p}=k_\mathrm{p}[\mathrm{P_n\cdot}][\mathrm{M}]
\]
\[
\unicode{x2234} \mathrm{[M]}=\frac{R_\mathrm{p}}{k_\mathrm{p}[\mathrm{P_n\cdot}]}
\tag4
\]
これは(3)式を変形しているだけですので、当たり前のことを言っていると思われるかもしれませんが、実際にMは開始反応でも消費されているため、\( \mathrm M\)は開始反応にも依存しますが、これを無視してしまい、成長反応にだけ依存すると仮定したということを表現しています。
なお、\( R_\mathrm i = k_\mathrm i [\mathrm I \cdot] [\mathrm M] \)と書かなかったのはそのためです。
仮定1より、生長ラジカルの反応性は重合度に依らないため、停止反応の反応系を\( 2\mathrm {P_n}\cdot\)と考えて反応速度を考えます。加えて\(k_\mathrm{tc} + k_\mathrm{td} = k_\mathrm t\)とし、停止反応を1つの式にまとめて表現します。
\[
\begin{align}
R_\mathrm{t}
&=k_\mathrm{tc}{[\mathrm{P_n\cdot}]}^2
+k_\mathrm{td}{[\mathrm{P_n\cdot}]}^2\\
&=(k_\mathrm{tc}+k_\mathrm{td}){[\mathrm{P_n\cdot}]}^2\\
&=k_\mathrm{t}{[\mathrm{P_n\cdot}]}^2
\tag5
\end{align}
\]
しかし、ラジカルは不安定で速やかに反応してしまうため、濃度計測が極めて困難です。そこで、\( [ \mathrm {P_n}\cdot ] \)を別の形で表現する必要があります。
仮定3より\(R_\mathrm i =R_\mathrm t\)であるため、
\[2k_\mathrm{d}f[\mathrm{I_2}]=k_\mathrm{t}{[\mathrm{P_n\cdot}]}^2\]
\[
\unicode{x2234}
[\mathrm{P_n\cdot}]=
\sqrt{
\frac{2k_\mathrm{d}f[\mathrm{I_2}]}{k_\mathrm{t}}
}
\tag6
\]
これを(3)式に代入して、
\[
R_\mathrm{p}=
\sqrt{
\frac{2k_\mathrm{d}f[\mathrm{I_2}]}{k_\mathrm{t}}
}[\mathrm{M}]
\tag7
\]
(7)式は重合初期段階においてよく一致することが知られています。
この式から、生長速度は開始剤濃度の0.5次に比例することがわかり、これは重合が2分子停止であることに対応しています。
このことから、(7)式はラジカル重合が存在することを実証する十分条件として考えられています。
(この説明を理解するには、反応速度論を学習しなければなりません。)
さて、生成するの高分子の数平均重合度\(P_\mathrm n\)は、
\[
\begin{align}
P_\mathrm{n} &= \frac{消費したモノマー数}{生成したポリマー数}\\
&=\frac{R_\mathrm{p}}{R_\mathrm{t}+R_\mathrm{tr}}\\
&=\frac{k_\mathrm{p}[\mathrm{P_n\cdot}][\mathrm{M}]}
{
k_\mathrm{t}{[\mathrm{P_n\cdot}]}^2+k_\mathrm{tr}[\mathrm{P_n\cdot}][\mathrm{XY}]
}
\tag8
\end{align}
\]
逆数をとって、
\[
\frac{1}{P_\mathrm{n}}=
\frac{k_\mathrm{t}[\mathrm{P_n\cdot}]}{k_\mathrm{p}[\mathrm{M}]}+
\frac{
k_\mathrm{tr}[\mathrm{XY}]
}
{
k_\mathrm{p}[\mathrm{M}]
}
\tag9
\]
(6)式を代入して、
\[
\frac{1}{P_\mathrm{n}}=
\frac{k_\mathrm{t}R_\mathrm{p}}{{k_\mathrm{p}}^2{[\mathrm{M}]}^2}+
\frac{k_\mathrm{tr}[\mathrm{XY}]}{k_\mathrm{p}[\mathrm{M}]}
\tag{10}
\]
しばしば\(C:=k_\mathrm{tr}/k_\mathrm{p}\)とおくことがあり、\(C\)を連鎖移動定数と言います。
\(C\)を用いて(10)式を書くと次のようになります。
\[
\frac{1}{P_\mathrm{n}}=
\frac{k_\mathrm{t}R_\mathrm{p}}{{k_\mathrm{p}}^2{[\mathrm{M}]}^2}+
\frac{C[\mathrm{XY}]}{[\mathrm{M}]}
\tag{11}
\]
(11)式を見ると、\(C\)が大きい、すなわち生長反応よりも連鎖移動反応のほうが起こりやすいほど、数平均重合度が小さくなることがわります。
このようなことから、高分子を合成する際は連鎖移動定数の小さなモノマー、開始剤、溶媒などを用いる必要があります。
逆に、あえて連鎖移動定数の大きな溶媒等を入れることによって重合を意図的に制御することもできます。
例えば、市販のスチレンにはカテコールという連鎖移動定数の大きな化合物が添加されており、光や熱によって勝手に重合が進むことを抑制しています。
このような目的で添加される化合物を重合禁止剤と言います。
最後に仮定4について説明して終わりにします。
連鎖移動反応は反応経路が複数考えられる一方、反応速度が一般に遅いため、無視してしまうというのが仮定4です。
