古典論の限界
現在の科学は量子力学によるところが非常に大きいです。
量子力学とは、極めて小さなものを扱う物理学で、高校で学んだ力学では扱えない範囲です。19世紀の終わり頃、量子力学が誕生する前のことですが、今では古典物理学と呼ばれる力学や電磁気学がほぼ完成し、世の中のすべての事象は説明できるようになったと考えられていました。
当時、まさかその根本原理が覆ると気付く人はほとんどいなかったと思います。20世紀初頭、相対性理論と量子力学が誕生しました。
まず、アインシュタインが空間と時間に関する科学者の考えを全面的に変え、古典的な考え方を拡張して光に近い速度と天文学的距離についても考えることができるようになりました。
一方、アインシュタインが一人で相対論を築いたのとは対照的に、多くの科学者が数十年にわたり古典的な考えを拡張した量子力学は、原子を構成する粒子、原子、および分子のふるまいを記述するために持ち込まれました。
現代では相対性理論が化学系へ与える影響は多く知られていないため、一般に物理化学では教えられません。しかし、量子力学は現代の原子構造や化学結合の根本原理となっており、量子力学を学ばずして現代の化学を学ぶことは不可能です。
なお、量子力学を化学に適応した学問を量子化学といいます。
リュードベリの式
いつ頃からかは定かではありませんが、どんな原子でも高温にしたり、あるいは放電したりするとその原子に固有の振動数を持つ電磁波が放出されることが知られています。
電磁波を波長ごとにわけて並べたものをスペクトルと言いますが、水素の発光スペクトルは経験的にリュードベリの式を満たすことが知られています。
放出される電磁波の波長を\(\lambda\)、正の整数を\(n\), \(n’\)(\(n<n’\)、\(R\)をリュードベリ定数とすると、以下のリュードベリの式が成立します。
\[\frac{1}{\lambda} = R \left( \frac{1}{n} – \frac{1}{n’} \right)\]
言い換えると、この式を満たす電磁波しか放出されません。
ド・ブロイ波
光は電磁波ですが、光が粒子のような挙動を示すような実験事実も多いです。この、光と波の両方の性質を二重性と言います。アインシュタインが発見した光電効果はそれを示す代表例です。
波が粒子のようなふるまいをするのであれば、粒子も波のようにふるまうのではないかと考えた人がいました。
当時大学院博士課程に在籍していたド・ブロイは、アインシュタインが相対性理論によって発見した次の式を改良して、粒子が波としてどれくらいの波長を持つかを考えました。
アインシュタインは、相対性理論から、光子（光を粒子として捉えたときの呼び方）の波長を\(\lambda\)、運動量を\(p\)とすると、プランク定数\(h\)を用いて次の式が成り立つことを示していました。
\[ \lambda = \frac{h}{p}\]
ここに、粒子の運動量mvを代入して、次の式が成り立つと主張しました。
\[ \lambda = \frac{h}{mv}\]
このようにして求められる波長をド・ブロイ波長と言います。実際にド・ブロイ波長は観測することができます。
ド・ブロイはこの研究を博士論文として提出しましたが、当時の教授たちは論文の内容を理解できなかったそうです。
そこで、ある教授がこの論文をアインシュタインに見せたところ、「博士号よりノーベル賞を受けるに値する」と返答したと言われています。実際、彼がこの論文を提出して5年後、ド・ブロイはノーベル化学賞を受賞しました。
水素のスペクトルとボーアモデル
デンマークの物理学者ボーアは、水素原子のスペクトルを説明できる水素原子のモデルを提案しました。
水素原子の中心には1つの陽子があり、その周りを電子が回っていると仮定します。また、陽子の重さは電子の重さの約1840倍と大きいため、陽子は動かないと仮定します。
\(r\)を軌道の半径、\(e\)を電気素量、\(k\)をクーロン定数とすると、電子にかかる力の大きさ\(F\)は次の式を満たします。
\[ F = k \frac{e^2}{r^2} \]
また、速さ\(v\)で等速円運動をしていると仮定すると、電子の質量\(m\)を用いて次の式も成り立ちます。
\[ F = m \frac{v^2}{r} \]
よって、次の式が成り立ちます。
\[ k \frac{e^2}{r^2} = m \frac{v^2}{r} \tag1 \]
ボーアの偉大な業績は、以下の2つの仮説を提唱したことです。
- 量子条件
電子の角運動量の大きさは次のように表せる。
\[ m r v = n \cdot \frac{h}{2\pi} \]
実は、この式を変形すると次のようになります。
\[ 2 \pi r = n \cdot \frac{h}{mv} \]
これは、ド・ブロイ波長の整数倍が円周の長さに一致することを意味しています。逆に整数倍が円周の長さに一致しないと、波が重なって最終的に波が消えてしまうので、この仮説は妥当であると考えられます。しかし、ド・ブロイの研究が発表されたのはボーアモデルが発表された後のことだったため、当時のボーアは知る由もなかったのです。 - 振動数条件
水素原子で放出される電磁波のエネルギーは、あるエネルギー状態から他のエネルギー状態へ遷移した時のエネルギーに等しい。
まず、量子条件から、
\[ v = \frac{nh}{2 \pi m r} \]
これを(1)式に代入して、
\[ k \frac{e^2}{r^2} = m \frac{ \left( \frac{nh}{2 \pi m r} \right)^2}{r} \]
\[ r = \frac{h^2}{4 \pi^2 e^2 k m} n^2 \tag2 \]
さて、電子と陽子の位置エネルギー\(V\)は、無限遠点を基準にすると、
\[ V = -k \frac{e^2}{r}\]
よって、電子の全エネルギー\(E\)は
\[E=\frac{1}{2} m v^2 -k \frac{e^2}{r} \tag3\]
(1)式より、\(mv^2=ke^2/r\)だから、これを(3)に代入して
\[ \begin{align}
E &= \frac{1}{2} \cdot k \frac{e^2}{r} -k \frac{e^2}{r} \\[5pt]
&= -\frac{ke^2}{2r}
\end{align}\]
ここに(2)式を代入すると、
\[
E = -\frac{2 \pi^2 e^4 k^2 m}{h^2} \cdot \frac{1}{n^2} \tag4
\]
よって、振動数条件から、整数\(n\)の値が\(n’\) から\(n\)になったとき見られる電磁波の波長は、
\[\frac{1}{\lambda} = \frac{2 \pi^2 e^4 k^2 m}{h^2}\left( \frac{1}{n} – \frac{1}{n’} \right)\]
そして、この定数の値を計算すると、見事リュードベリ定数と一致します。
ボーアモデルは量子力学的にはかなり不完全なモデルですが、量子力学から求められる種々の事実がこの不完全なモデルでもわかる点で魅力的であることから、今でも学ばれ続けているのだと思います。
まず、\(n=1\)における原子半径は、(2)式より
\[r = \frac{h^2}{4 \pi^2 e^2 k m} 1^2 = 0.053\ \mathrm{nm}\]
この値は量子力学で求めた値に等しいことが知られています。また、この値をボーア半径と言います。
次に、(2)式より原子半径は\(n^2\)に比例し、(4)式よりエネルギーは\(-1/n^2\)に比例することがわかります。つまり、原子半径はnが増えるごとに半径は一気に大きくなる一方、エネルギーは\(n\)が大きくなるごとに大きくなってはいくものの、その値は近接したものになっていきます。
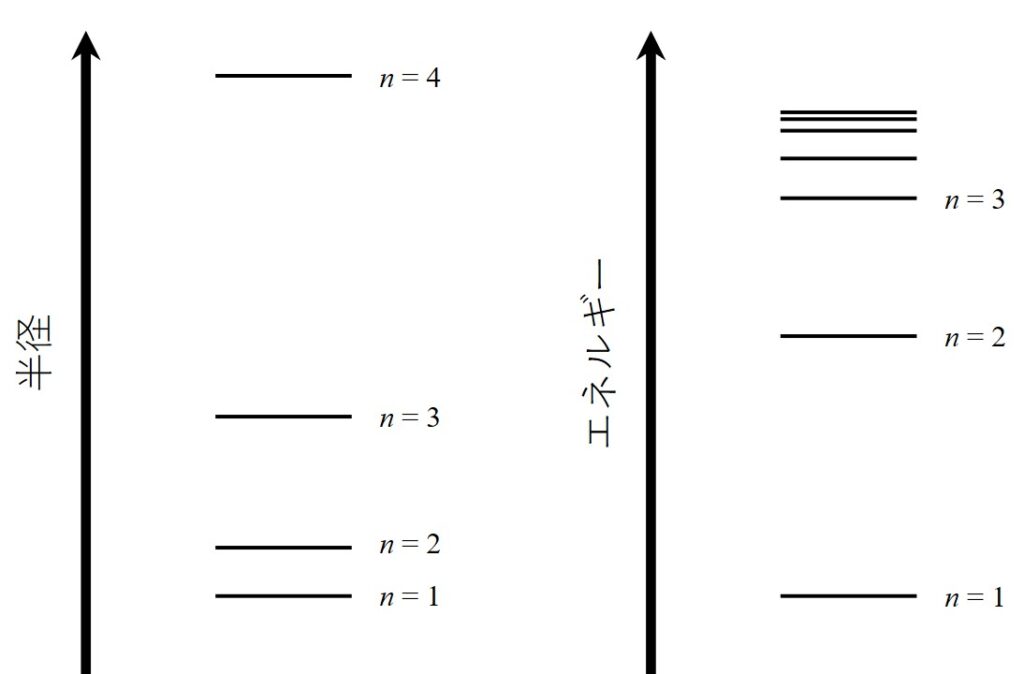
これは量子力学的にも正しく重要な結果なため、覚えておくとよいかと思います。
ハイゼンベルグの不確定性原理
1個の電子の位置を測定する場合を考えてみます。距離Δx以内に電子の位置を決めようとすると、\(\lambda \approx \Delta x \)の電磁波を当てると相互作用から電子の位置が分かると考えられます。
光子の運動量は\(h/\lambda\)で、撃力によってこの運動量の一部が電子に移動します。すなわち、電子を見つけるという操作が運動量に変化を及ぼします。
もし、もっと正確に電子の位置を決めようとすれば、さらに短い波長の光を使えばよいことになります。この結果、運動量はずっと大きな値になります。
ハイゼンベルクは、この過程を注意深く分析し、どれだけの運動量が電子に移動した蚊を正確に決めることは不可能であることを明らかにしました。
電子の位置を複数回計測したときにおける、電子の位置の標準偏差と運動量の標準偏差をそれぞれ\(\sigma_x\), \(\sigma_p\)とすると、次の式が成り立つことを示しました。
\[ \sigma_x \sigma_p \geq \frac{\hbar}{2}\]
ここで、\(\hbar = h/2\pi\)で定義され、これをディラック定数や換算プランク定数などと呼びます。
この式は、どんな粒子でも位置を標準偏差\(\sigma_x\)の範囲で決めようとすると自動的に粒子の運動量に不確かさが生まれ、その大きさが上式で表されるという意味です。
古典力学では位置が決まらない、あるいは運動量が決まらないということは古典論ではありえないことで、直感に反する結果です。