熱力学を勉強していると、断熱自由膨張でのエントロピー変化を計算させる問題をよく見かけます。
実際、化学系の私は物理化学の授業を受けているときに演習問題として断熱自由膨張に出会いました。
その際、断熱過程なのでエントロピー変化が0である、と答えたくなるのですが、実はエントロピーは正の値をとります。
本記事では、断熱自由膨張でのエントロピー変化について解説します。
断熱自由膨張とは
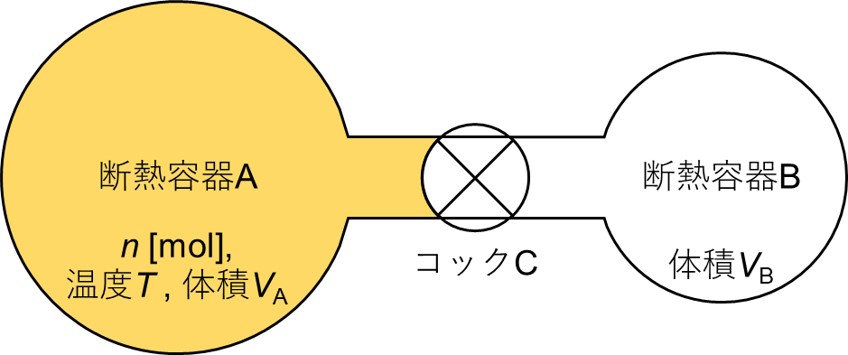
体積がそれぞれ\(V_A\)と\(V_B\)の断熱容器Aと断熱容器Bを、コックCでつなげます。また、外界の温度は\(T\)で一定であるとします。
加えて、断熱容器Aには温度\(T\)の理想気体を\(n\)モルいれ、断熱容器Bは真空にしておきましょう。
いま、コックCを開けると、断熱容器Aに入っていた気体が断熱容器Bに流れ、平衡状態に達しました。
このように、気体が仕事をせずに膨張することを自由膨張といい、特にそれが断熱過程で起こる時は断熱自由膨張といいます。
このとき、理想気体のエントロピー変化はどのように計算したらよいでしょうか?
*補足
仕事をしていない?体積が増えているのに?と思った方もいるかもしれません。そのような方は、仕事の定義を思い出してください。仕事\(W\)は、外圧\(P_\mathrm{ex}\)を用いて定義されるのでした。系の体積を\(V_\mathrm i\)から\(V_\mathrm f\)まで変化させるときの仕事は、
\[
W=-\int_{V_\mathrm i}^{V_\mathrm f} P_\mathrm{ex}dV
\]
今回の場合、断熱容器Bは真空だったので、\(P_\mathrm{ex}=0\)です。そのため、\(W=0\)なのです。
外界の圧力と系の圧力の差があると仕事をするはずなので、仕事の大きさを外圧で定義するのはおかしいのではないかと思う方もいらっしゃるでしょう。しかし、そこで合わない分は熱として勘定されるので、実は問題ないのです。
熱力学的なエントロピーの計算
断熱自由膨張でのエントロピー変化を求めるとき、熱の出入りが0だからエントロピーは0と結論付けてしまいたくなるのですが、これは間違っています。
エントロピーは、可逆過程で定義される値です。そのため、題意の状態変化ができるような可逆過程を自分で探し出し、そのエントロピー変化を計算する必要があります(題意の状態変化は不可逆です)。
今回は、温度が一定なので、等温可逆膨張のエントロピー変化の公式を借りて、本問題のエントロピー変化\(\Delta S\)を計算しましょう。
\[
\Delta S = nR \ln \frac{V_\mathrm A + V_\mathrm B}{V_\mathrm A}
\]
\(V_\mathrm A + V_\mathrm B > V_\mathrm A\)なので、\(\Delta S > 0\)になります。
それでも納得できないあなたへ: \(S=k \ln W\)
断熱自由膨張でのエントロピー変化は、ボルツマンの式を使って計算することもできます。先ほどの熱力学的な解き方で腑に落ちない方もいらっしゃるかもしれません。そのような方は、こちらを参考にしてみてください。
ボルツマンの式とは次のような式のことでした。エントロピー\(S\)、ボルツマン定数\(k\)、状態数\(W\)を用いて、
\[
S=k \ln W
\]
ここで、状態数とは「あるエネルギーにおける系のとり得る場合の数」のことです。何を言っているのかよくわからないと思いますので、問題を解きながら詳しく説明する形にします。
まず、膨張前のエントロピーについて考えます。膨張前における気体の体積\{V_\mathrm A\}を、無限小の体積\(v\)で分割し、その区画に\(n\)モルの気体を配置することを考えます。つまり、区画の数は\(V_\mathrm A / v\)個です。なお、体積\(v\)にいくらでも分子を入れていいものとします。
このとき、アボガドロ数を\(N_\mathrm A\)とすると、\(n\)モルの気体が配置される場合の数\(W_1\)は、重複順列の考え方から次のようになります。
\[\begin{align}
W_1=
\left(
\frac{V_\mathrm A}{v}
\right)^{nN_\mathrm A}
\end{align}\]
よって、膨張前のエントロピー\(S_1\)は次のようになります。
\[\begin{align}
S_1=k \ln
\left(
\frac{V_\mathrm A}{v}
\right)^{nN_\mathrm A}
\end{align}\]
同様にして、膨張後のエントロピーは次のように計算できます。
\[\begin{align}
S_2=k \ln
\left(
\frac{V_\mathrm A + V_\mathrm B}{v}
\right)^{nN_\mathrm A}
\end{align}\]
以上より、断熱自由膨張でのエントロピー\(\Delta S\)は、
\[\begin{align}
\Delta S &= S_2-S_1 \\
&=k \ln
\left(
\frac{V_\mathrm A}{v}
\right)^{nN_\mathrm A}
–
k \ln
\left(
\frac{V_\mathrm A + V_\mathrm B}{v}
\right)^{nN_\mathrm A}\\
&=knN_\mathrm A \ln \frac{V_\mathrm A + V_\mathrm B}{V_\mathrm A}\\
&=nR \ln \frac{V_\mathrm A + V_\mathrm B}{V_\mathrm A}
\end{align}\]
見事、熱力学的な計算と同じ値になりました。
最後に、状態数について補足します。状態数とは「あるエネルギーにおける系のとり得る場合の数」でした。場合の数については、上記の計算を例に紹介しましたが、「あるエネルギーにおける」という部分には触れていません。
断熱自由膨張では、熱の出入りがなく、仕事もないので、熱力学第一法則より\(\Delta U=0\)です。つまり、膨張前後で内部エネルギーは変化しません。このように、エネルギー状態に変化のないような組み合わせで、エントロピー変化の計算が可能になります。
このあたりの話は、統計力学をしっかりと学ばないとわからないところなので、これくらいにしておきます。
悩んだら「乱雑さ」を考えよう!
断熱自由膨張でのエントロピー変化についての説明は以上になります。
もし、この話を忘れてしまったときは、乱雑さについて考えてみてください。コックを開けて気体が広がる方がより乱雑になるので、エントロピー変化は正だということがわかるかと思います。
