当記事では、化学系の学生さん向けに、エントロピーがどのようにして導かれるかを解説します。
私が大学で物理化学を勉強した時は、(熱力学的な)エントロピーは定義として与えられ、なぜそのような定義になるの?と思っていました。
本記事が、同じようなことを思われている学生さんの一助になれば幸いです。
前提知識
エントロピーの定義について知るためには、カルノーサイクルや熱力学第二法則、カルノーの定理についての知識が必要になります。当サイトにはこれらのことについて解説した記事がございます。こちらを是非ご覧ください。
エントロピーの導出
可逆機関\(C_i (i=1, 2, \cdots,n)\)を\(n\)個用意し、熱浴を\(\mathrm R\)、任意の熱機関を\(\mathrm C\)として、次のような装置を組み立てます。
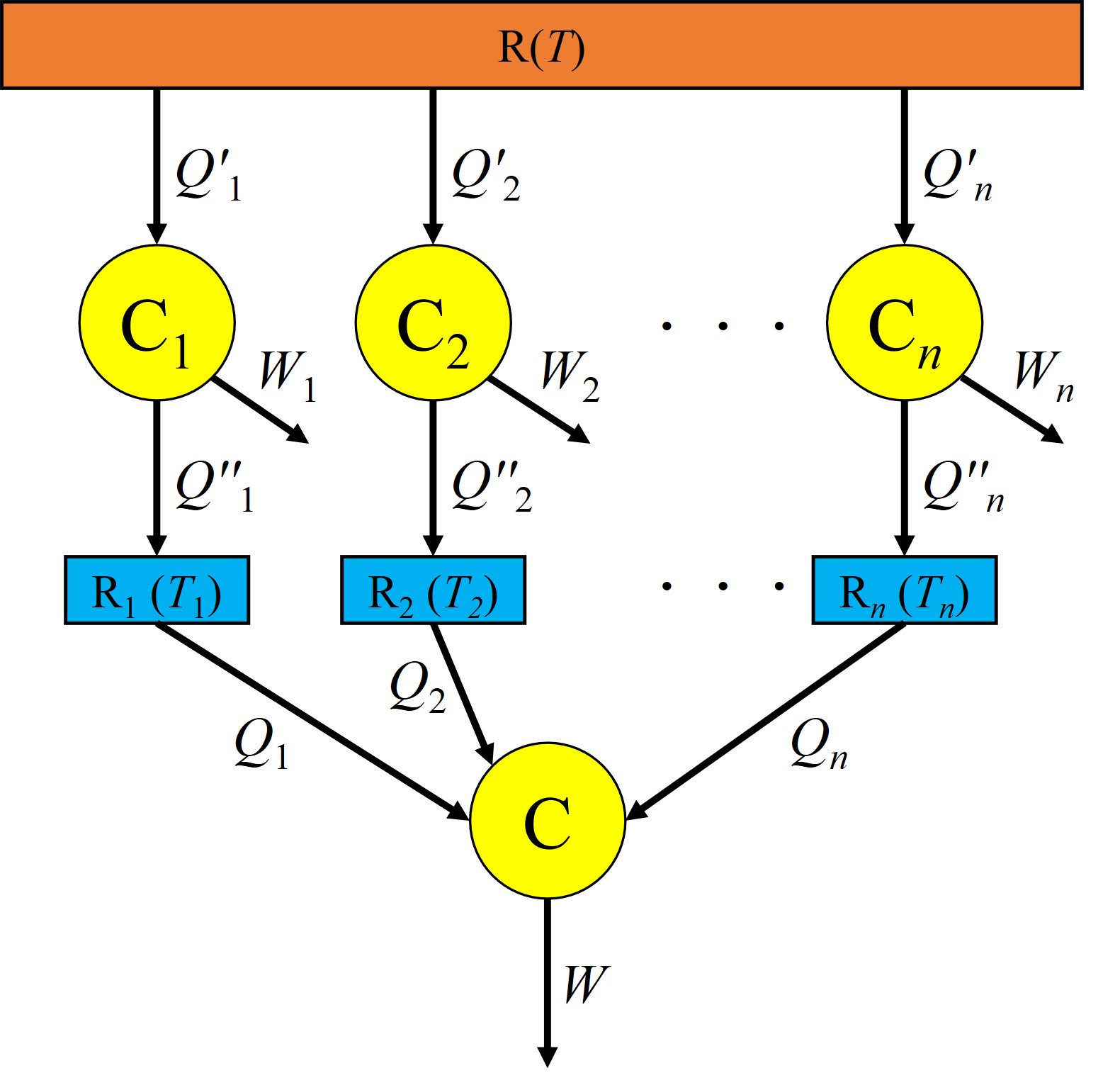
なお、熱浴\(\mathrm R\)の横に書いてある\(T\)が温度を表し、\(Q\)は熱、\(W\)は仕事を意味します。
一見すると、\(\mathrm C\)はすべての熱を仕事に変えているように見えますが、いくつかの\(Q_i\)は負の値だとして考えます。つまり、\(C_i\)の中には逆サイクルもあります。
前提知識として紹介した記事にあるように、カルノーの定理から次の式が導かれるのでした。
\[
\frac{Q_\mathrm{H}}{T_\mathrm{T}} + \frac{Q_\mathrm{L}}{T_\mathrm{L}} \leq 0
\tag1
\]
これを図1に適用します。可逆機関において、(1)式では等号が成り立ちます。
\[\frac{{Q_i}^{\prime}}{T} + \frac{{Q_i}^{\prime \prime}}{T_i} = 0\]
\(i=1\)から\(n\)で和をとって、
\[
\frac{1}{T} \sum_{i=1}^n {Q_i}’ + \sum_{i=1}^n\frac{{Q_i}^{\prime\prime}}{T_i} = 0
\]
\[\Leftrightarrow \frac{1}{T} \sum_{i=1}^n {Q_i}’ = – \sum_{i=1}^n \frac{{Q_i}^{\prime\prime}}{T_i}
\tag2\]
また、\(\mathrm C_i\)で熱力学第一法則を考えると、次式が成り立ちます。
\[{Q_i}’ + {Q_i}^{\prime\prime} = W_i\]
\(i=1\)から\(n\)で和をとって、
\[\sum_{i=1}^{n}{Q_i}’ + \sum_{i=1}^{n}{Q_i}^{\prime\prime} = \sum_{i=1}^{n}W_i
\tag3\]
\(\mathrm C\)についても同様に考えると、
\[
\sum_{i=1}^{n}Q_i = W
\tag4
\]
(3)+(4)より、
\[
\sum_{i=1}^{n}{Q_i}’ + \sum_{i=1}^{n}Q_i + \sum_{i=1}^{n}{Q_i}^{\prime\prime} = \sum_{i=1}^{n}W_i +W
\]
ここで、\({Q_i}^{\prime\prime} = -Q_i\)とすると、
\[
\sum_{i=1}^{n}{Q_i}’ = \sum_{i=1}^{n}W_i +W
\]
ところで図1を全体的に俯瞰してみると、熱浴\(\mathrm R\)と、(n\)個の\(\mathrm C_i\)と\(\mathrm C\)からなる大きな熱機関から構成されていることがわかります。もし\(\sum_i {Q_i}’ > 0\)だと、すべての熱を仕事にしてしまう、トムソンの原理に反する熱機関ができてしまいます。そのため、次の不等式を満たす必要があります。
\[
\sum_{i=1}^{n}{Q_i}’ \leq 0
\tag5
\]
Cが可逆なとき、系全体が可逆サイクルからなるため、逆方向のサイクルも可能となります。ここで\(\sum_i Q < 0 \)とすると、その逆サイクルは\(\sum_i Q > 0 \)となってしまい、これはトムソンの原理に反することになります。そのため、\(\sum_i Q = 0 \)であることが必要です。
Cが不可逆な時、すなわち逆サイクルがトムソンの原理に反する時、上述の通り、\(\sum_i Q < 0 \)です。
以上より、Cが可逆なときは等号、不可逆な時は不等号が成り立つことがわかります。
さて、(2)式に\({Q_i}’ = -{Q_i}’\)を代入することで、熱が入る方向を正、出ていく方向を負に直し、次いで(5)式の不等式を用いると、
\[
\frac{1}{T} \sum_{i=1}^n {Q_i}’ = \sum_{i=1}^n\frac{{Q_i}^{\prime\prime}}{T_i} \leq 0
\]
このようにして、(1)式を拡張することができました。
\[
\sum_{i=1}^n\frac{{Q_i}^{\prime\prime}}{T_i} \leq 0
\tag6
\]
\(n \to \infty\)のとき、(6)式は積分で表すことができます。
\[
\oint \frac{{Q_i}^{\prime\prime}}{T_i} \leq 0
\tag7
\]
インテグラルに丸がついた記号は、積分の始点と終点が同じことを意味します。このような積分を周回積分といいます。
さて、Cが可逆な時は等号が成立するということですが、これはつまり、サイクルを一周させると元に戻るため、状態関数であるとわかります。
このようなことから、エントロピーが定義されます。
可逆的に入ってくる熱を\(Q\)として、
\[\mathrm dS = \frac{\mathrm d’Q}{T}\]
積分形で表記すると、基準の状態OからAへ変化するとき、
\[S = \int_O^A \frac{\mathrm d’Q}{T}\]
ポイントは、熱が可逆的に入ってくるということです。可逆過程のときのみ、周回積分が0になり、\(\mathrm d’Q / T\)が状態関数となります。状態関数は経路や履歴に依存しないため何かと便利です。わざわざ可逆過程を仮定しているのはそのためです。
また、エントロピーの定義は線積分ではなくなりました。熱力学サイクルという、最終的には初めの状態に戻るような循環的な操作を考えた結果、線積分が出てきたわけですが、(7)式を片道切符でも定義できるようにしたということです。
エントロピー増大則とは
「エントロピーは増大する!」という言葉を聞いたことはあるでしょうか。あるいは、「エントロピーが増大するから部屋が散らかっていてもしょうがないんだ!」とおっしゃる方もいるかもしれません。この、エントロピーが増大するという話について解説します。
エントロピーは可逆過程でしか定義されていませんでしたが、不可逆過程でエントロピー変化を無理やり計算してみましょう。状態Xから状態Yへ不可逆的に変化したときのエントロピー変化は、この過程を可逆的に変化させたときのエントロピー変化\(\Delta S= S(\mathrm Y)-S(\mathrm X)\)であるとします。
XからYへの不可逆過程を\(\Gamma_1\)、YからXへの可逆過程を\(\Gamma_2\)と名づけることにします。
いま、状態Xから過程\(\Gamma_1\)を経由して状態Yにし、そこから過程\(\Gamma_2\)で状態Xに戻ってくるサイクルを考えます。このサイクルは途中に不可逆過程を含むため、サイクル全体としては不可逆過程です。したがって、(7)式より線積分は負になるため、
\[
\begin{align}
\oint \frac{\mathrm{d}’Q_i}{T} &= \int_{\Gamma 1} \frac{\mathrm{d}’Q_i}{T} + \int_{\Gamma _2} \frac{\mathrm{d}’Q_i}{T}\lt 0\tag8
\end{align}
\]
ここで、過程\(\Gamma_2\)は可逆なので、状態X, Yでのエントロピーをそれぞれ\(S_{\mathrm X}\)、\(S_{\mathrm Y}\)とすると、(8)式は次のように表せます。
\[
\int_{\Gamma _1} \frac{\mathrm{d}’Q_i}{T} + \left\{ S(\mathrm{X}) -S (\mathrm{Y}) \right\}\lt 0
\]
\[
S(\mathrm{Y}) -S (\mathrm{X}) \gt \int_{\Gamma _2} \frac{\mathrm{d}’Q_i}{T}
\]
断熱系では\(\mathrm d’Q_i=0\)であるため、
\[
S(\mathrm{Y}) -S (\mathrm{X}) \gt 0
\tag9
\]
(9)式はどうやって解釈しましょう?これは、前述した不可逆過程において無理やり定義したエントロピー変化になっています。したがって、以下のように主張できます。
断熱系における不可逆過程ではエントロピーが増大する。
なお、化学系の教科書では「孤立系」での不可逆仮定でエントロピーが増大すると書かれていることが多いです。
孤立系は断熱系の一つなので問題ないのですが、正確には断熱系での話なのです。孤立系と書かれている理由は、宇宙が孤立系であると考えられているからだと思います。
クラウジウスは、「宇宙のエントロピーは最大値に向かう」と言ったため、それにあやかりこのような表現をしているのだと思います。
ここまで、可逆過程と不可逆な断熱過程からなるサイクルを使って、エントロピー増大則を導きました。
なるほど、「可逆過程と不可逆な断熱過程からなるサイクルに限って」断熱系における不可逆過程ではエントロピーは増大するのか、と思った方もいるかもしれませんが、、、
ちょっと待った!!
実際に可逆過程と不可逆な断熱過程の二つを含んでいなくても、断熱系における不可逆過程ではエントロピーが増大します!!単に不可逆な断熱過程が起こるだけでもエントロピーは必ず増大します!!
なぜかというと、不可逆過程のエントロピー変化は、可逆過程のエントロピー変化を借りて計算するからです。可逆過程のエントロピー変化をお借りする以上、サイクルを考えざるを得ないのです。
例えば、何か適当な不可逆過程を起こしたとしましょう。この時のエントロピー変化を考える際は、可逆的に熱が入ってきたと仮定して(頭の中で想像して)、その際のエントロピー変化を採用するのでした。
したがって、不可逆過程のエントロピー変化を考える場合、可逆過程と不可逆過程の二つを絶対に考えることになります。
そして、可逆過程は逆の過程も可能なので、不可逆過程のエントロピーを考えるときは必ずクラウジウスの不等式が使えると言い換えることができます。
以上のことから、エントロピー増大則は、考えている過程がサイクルかどうかに関係なく適応できます。
かくいう私も、エントロピーが増大する理由がよくわからずに苦しんでいました。エントロピーは増大すると言っているのに、クラウジウスの不等式によれば0か負になると言っているではないか!!何事だ!!と思っていました。
つまり、 \( \mathrm dQ/T\)がエントロピーなのだと勘違いしていたのです。可逆的に熱が出入りしている場合に限って\( \mathrm dQ/T\)がエントロピーと等しいということに気づくのには時間がかかりました。
統計力学エントロピー
ここまでエントロピーについてみてきましたが、「エントロピーが増大するから部屋が散らかっていてもしょうがないんだ!」についての解説には至っていません。これを理解するためには、統計力学の力を借りなければなりません。
熱力学は、分子一つ一つについては全く考えずにマクロな系を語る学問です。一方、統計力学は、分子一つ一つを見ることによってマクロな系を語ります。
化学系の教科書では統計力学を統計熱力学と表記することが多いです。また、化学で統計力学を学ぶことは稀ですが、統計力学的なエントロピーの解釈に関しては必ずと言っていいほど学びます。
統計力学によると、エントロピーは次のように表せます。これをボルツマンの原理といいます。
\[S = k_\mathrm{B} \ln W\]
ここで、\(k_\mathrm{B}\)はボルツマン定数、\(W\)は状態数である。
状態数とは何でしょうか。ここでは、「全体のエネルギーを変化させずに変えることのできる場合の数」としておきます。
化学系の学生さんであれば、これ以上の詳しいことは知る必要はないように感じます。物理化学系の研究室で研究することになったら、またそのときに勉強すればよいと思います。
簡単に説明すると、どこかの場所に局在化する場合の数よりも、全体に広がる場合の数のほうが大きいということです。
これがいわゆる乱雑さです。この式の使い方は、以下の記事で簡単に説明しているので、興味があればこちらをご参照ください。
