化学系の学生さんで物理に苦手意識のある方は多いように感じます。特に、エントロピー関連のトピックや量子化学はとりわけ難しく、つまずいてしまうこともあるかと思います。
当記事では、化学系の方でもわかるように熱力学第二法則を説明します!
熱機関
熱機関とは、熱を加えるか吸収することで状態変化を起こし、再び初期状態に戻す操作(熱サイクル)によって仕事を取り出す仕組みのことを言います。
例えば、気体の入ったストンに熱を加え体積を膨張させ、放冷して元の状態に戻せば、それは熱サイクルです。
熱源を二つ用意し、温度の高い方を高温熱源、低い方を低温熱源とし、熱サイクルをCとします。これらをまとめて熱機関といいます。
いま、熱サイクルが吸収した熱を\(Q_\mathrm{in}\)、放出した熱を\(Q_\mathrm{out}\)、正味の仕事を\(W\)とすると、熱機関の概念図は次のように描けます。
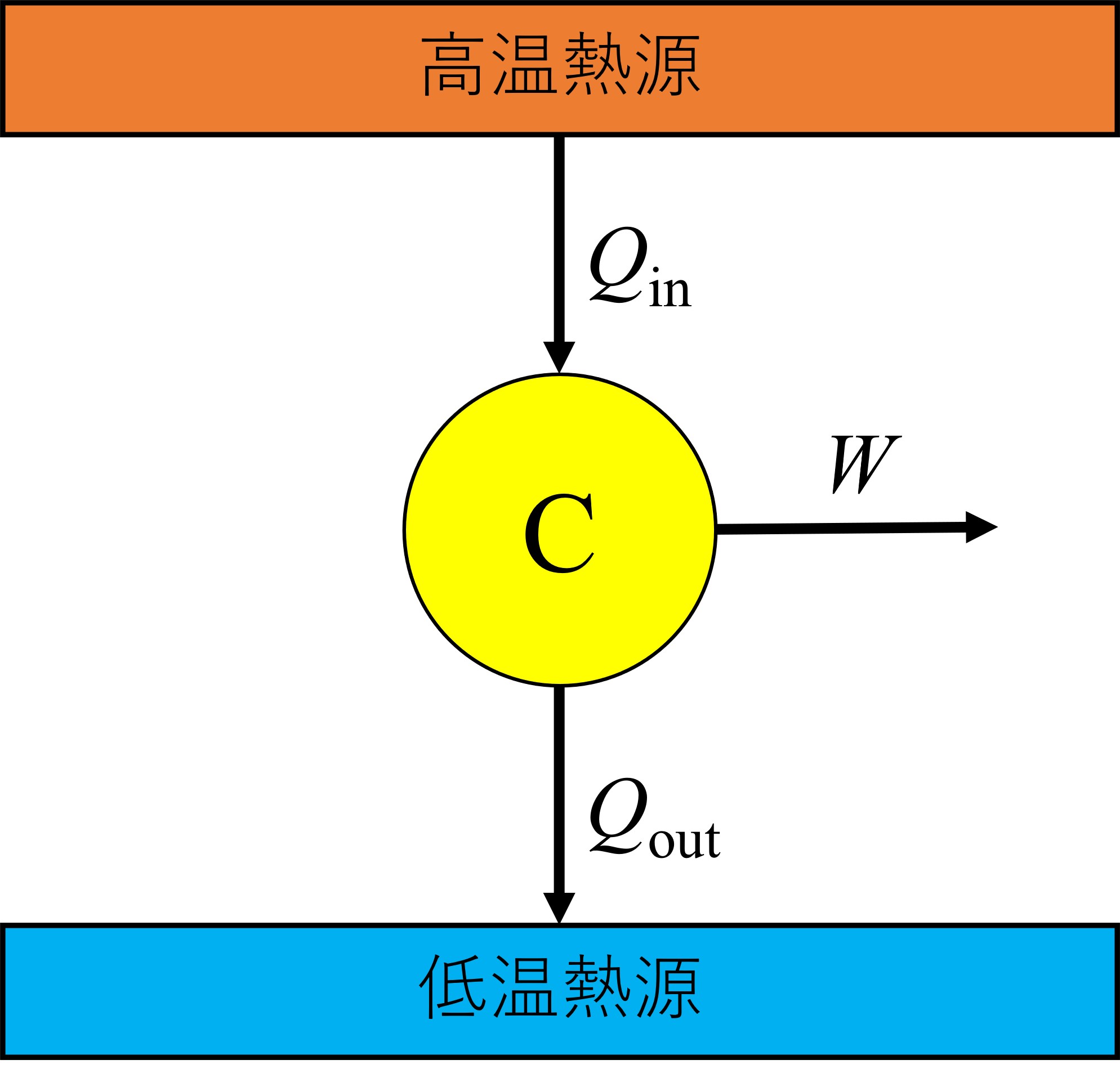
なお、正味の仕事とは、外界にした仕事から系にした仕事を差し引いた値です。
熱サイクルは考えようと思えば無限に考えられるわけですが、カルノーサイクルはこれからエントロピーを考える上で非常に重要な熱サイクルです。
カルノーサイクルは、等温可逆変化、断熱可逆変化、等温可逆変化、断熱可逆変化の順に変化させ、初期状態に戻る熱サイクルです。
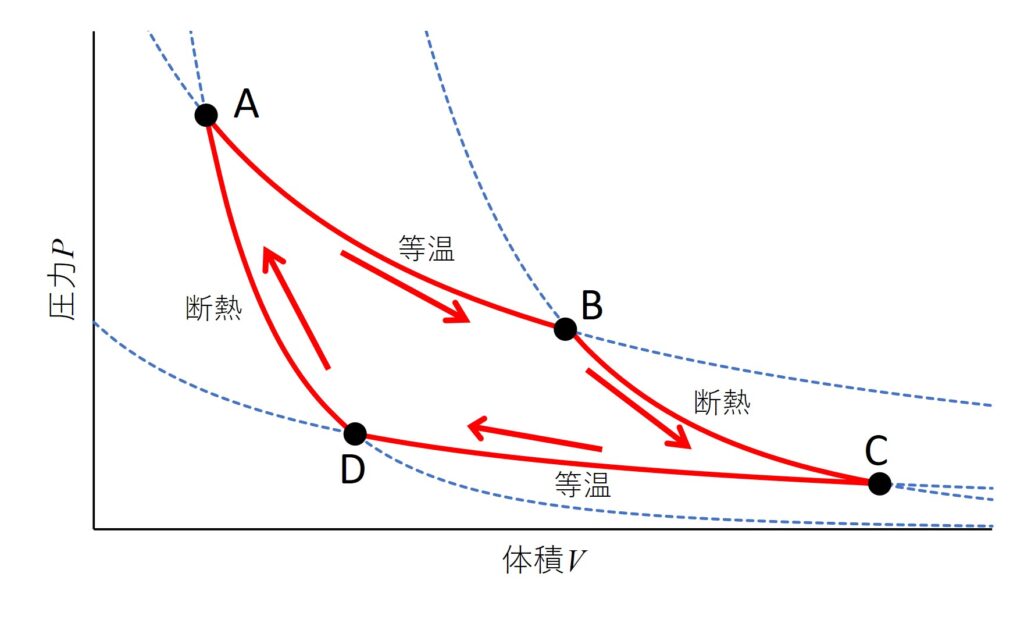
なお、上記の図2においては、点線は\(V=0\)で無限大に発散するため、本来ならば縦軸と交わりません。
ここではサイクルの形をお見せしたかったため、縦軸をずらして描写しています。ご注意ください。
さて、サイクルの形は熱源の温度や比熱比によって変わります。また、カルノーサイクルとは逆順の熱サイクルを逆カルノーサイクルといいます。
なお、熱源から熱を奪う、又は与えると熱源の温度が変わるはずですが、計算が煩雑になってしまうため、熱源の温度は変わらないと考えます。このように、熱容量が無限大の熱源を熱浴といいます。
ではカルノーサイクルにおけるそれぞれでの過程での仕事と熱を計算します。状態\(\mathrm {X (X=A,B,C,D)}\)での体積を\(V_\mathrm X\)、\(\mathrm{A,B}\)での温度を\(T_\mathrm H\)、\(\mathrm {C,D}\)での温度を\(T_\mathrm L\)とし、状態変化\(\mathrm {X \to Y}\)での熱、仕事、内部エネルギー変化をそれぞれ\(Q_\mathrm {XY}, W_\mathrm {XY}, \Delta U_\mathrm {XY} \)とします。
また、熱を放出するときは\(Q_\mathrm{XY}<0\)、吸収するときは\(Q_\mathrm{XY}>0\)、外界に仕事をするときは\(W_\mathrm{XY}>0\)、系に仕事をするときは\(W_\mathrm{XY}<0\)とします。つまり、熱に関しては系に入る方向を正、仕事に関しては系から出る方向を正としています。
\(\mathrm{A \to B}\)では
\[
\Delta U_\mathrm{AB}=0,\quad
W_\mathrm{AB}=nRT_\mathrm{H}\ln{\frac{V_\mathrm{B}}{V_\mathrm{A}}},\quad
Q_\mathrm{AB}=W_\mathrm{AB}=nRT_\mathrm{H}\ln{\frac{V_\mathrm{B}}{V_\mathrm{A}}}
\]
\(\mathrm{B \to C}\)では
\[
Q_\mathrm{BC}=0,\quad
\Delta U_\mathrm{BC}=nC_\mathrm{v}(T_\mathrm{L}-T_\mathrm{H}),\quad
W_\mathrm{BC}=-\Delta U_\mathrm{BC}=-nC_\mathrm{v}(T_\mathrm{L}-T_\mathrm{H})
\]
\(\mathrm{C \to D}\)では
\[
\Delta U_\mathrm{CD}=0,\quad
W_\mathrm{CD}=nRT_\mathrm{L}\ln{\frac{V_\mathrm{D}}{V_\mathrm{C}}},\quad
Q_\mathrm{CD}=W_\mathrm{CD}=nRT_\mathrm{L}\ln{\frac{V_\mathrm{D}}{V_\mathrm{C}}}
\]
\(\mathrm{D \to A}\)では
\[
Q_\mathrm{DA}=0,\quad
\Delta U_\mathrm{DA}=nC_\mathrm{v}(T_\mathrm{H}-T_\mathrm{L}),\quad
W_\mathrm{DA}=-\Delta U_\mathrm{DA}=-nC_\mathrm{v}(T_\mathrm{H}-T_\mathrm{L})
\]
特に断りもなく計算してしまいましたが、熱サイクル内の物質が(作業物質)が「理想気体」であることを仮定して計算しました。これが後に紹介するカルノーの定理で重要になってきます。
もうひとつ、熱効率を紹介します。熱効率とは、吸収する熱量に対する正味の仕事の割合で、よく\(\eta\)で書き表されます。
\[
\eta=\frac{W}{Q_\mathrm{in}}
\]
また、サイクルで内部エネルギー変化\( \Delta U = 0\)なので、\(Q_\mathrm{in}-Q_\mathrm{out}=W\)です。したがって、熱効率は次のようにも表せます。
\[
\begin{align}
\eta &= \frac{Q_\mathrm{in}-Q_\mathrm{out}}{Q_\mathrm{in}}\\
&= 1-\frac{Q_\mathrm{out}}{Q_\mathrm{in}}
\end{align}
\]
さらに、可逆的な断熱過程ではポアソンの法則が成り立ちます。
\[
\begin{cases}
T_\mathrm{H}{V_\mathrm{B}}^{\gamma-1} = T_\mathrm{L}{V_\mathrm{C}}^{\gamma-1}\\
T_\mathrm{L}{V_\mathrm{D}}^{\gamma-1} = T_\mathrm{H}{V_\mathrm{A}}^{\gamma-1}
\end{cases}
\]
\[\unicode{x2234} \frac{V_\mathrm{C}}{V_\mathrm{D}}=\frac{V_\mathrm{B}}{V_\mathrm{A}}
\]
よって、理想気体を作業物質とするカルノーサイクルの熱効率は次のように計算できます。
\[
\begin{align}
\eta &= 1-\frac{-nRT_\mathrm{H}\ln{\frac{V_\mathrm{D}}{V_\mathrm{C}}}}{nRT_\mathrm{L}\ln{\frac{V_\mathrm{B}}{V_\mathrm{A}}}}\\
&= 1-\frac{T_\mathrm{L}}{T_\mathrm{H}}
\end{align}
\]
このように、カルノーサイクルの熱効率は熱浴の温度だけで決まります。これが後に紹介するエントロピーの定義で重要な役割を果たします。
クラウジウスの原理とトムソンの原理
ここで、ようやく熱力学第二法則の説明に移ります。熱力学第二法則には様々な表現方法がありますが、その中でもクラウジウスの原理とトムソンの原理について説明します。
他に何の変化も残さないように、低温熱源から高温熱源に熱を移すことはできない。
他に何の変化も残さないように、熱をすべて仕事に変える熱サイクルは存在しない。
例えば、冷水に熱水を入れると生ぬるい水にはなりますが、生ぬるい水が勝手に冷水と熱水に分かれることはありません。
熱とは温度の移動形態です。熱いものと冷たいものを触れさせて双方が間の温度になるとき、熱い方から冷たい方に熱は移動したと表現します。
エアコンのように、何らかの手を加えれば低温熱源から高温熱源に熱を移動させることはできます。この場合は電気エネルギーを使って熱を無理やり移動させているわけです。
しかし、「他に何の変化も残さないように」これをするのは無理だというのがクラウジウスの原理です。我々が当たり前に感じているいことを言語化したに過ぎないと考えてもよいのかもしれません。
トムソンの原理に関しては、直感的にはあまりピンと来ないのではないでしょうか。
実は、クラウジウスの原理とトムソンの原理は同値であることが知られています。以下でそれを証明します。
クラウジウスの原理を命題\(p\)、トムソンの原理を命題\(q\)、これらの否定をそれぞれ\(\bar p, \bar q\)とします。いま証明したいのは\(p \Leftrightarrow q\)なので、これと同値な\(p \Rightarrow q\)かつ\(q \Rightarrow p\)を示すことにします。
まず、\(p \Rightarrow q\)を示します。これは\(\bar q \Rightarrow \bar p\)と同値です。トムソンの原理を否定する熱機関は熱効率100 %で動きます。いま、低温熱源から得た熱を全て仕事に変え、その仕事を使って逆カルノーサイクルのような逆順のサイクルを動かし、高温熱源に熱を捨てることを考えると、他に何の変化も残さず低温熱源から高温熱源へ熱を移動させることができました。これはクラウジウスの原理に反します。以上より、\(p \Rightarrow q\)が真であることがわかりました。
次に、\(q \Rightarrow p\)を示します。 これは\(\bar p \Rightarrow \bar q\)と同値です。クラウジウスの原理を否定する熱サイクルは、他に何の変化も残さず低温熱源から高温熱源に熱を移すことができます。そのため、普通なら低温熱源に捨てられる熱を再び高温熱源に戻せば、熱効率が100 %の熱機関が出来上がり、これはトムソンの原理に反します。よって、\(q \Rightarrow p\)が真であることがわかりました。
このようにして、クラウジウスの原理とトムソンの原理が同値であることがわかりました。
ただし、注意していただきたいのは、クラウジウスの原理とトムソンの原理が同値であることがわかっただけで、これらの原理自体が正しいと主張しているわけではないということです。
これらの原理はあくまでも経験則ですので注意してください。また、統計力学を勉強すれば、このあたりの話がもう少し分かりますが、化学系の学生が学ぶことは少ないため、ここでは割愛します。
余談ですが、ここで経験則として受け入れている熱力学第二法則は、難しい物理学を使えば証明することができるようです。詳しいことは私もわからないのですが、これは学部生のレベルを優に超えていて、研究レベルの話になってきます。
カルノーの定理
クラウジウスの原理から、カルノーの定理という重要な定理が導かれます。
可逆な熱機関の熱効率\(\eta\)は、理想気体を作業物質としたカルノーサイクルの熱効率\(\eta^\prime\)に等しい。つまり、可逆な熱機関の熱効率は高温熱浴と低温熱浴の温度にのみ依存する。また、不可逆な熱機関の熱効率\(\eta^{\prime \prime}\)はこれよりも小さい。
\[
\eta^{\prime \prime}< \eta^{\prime} = \eta
\]
つまり、可逆的な熱機関の熱効率は最も大きく、その値はカルノーサイクルで示した高温熱源と低温熱源の温度で表されるということです。また、温度が無限になることはないので、熱効率は100 %になりません。
では、証明していきます。カルノーサイクルをC、任意の可逆的な熱サイクルをD、その逆サイクルをD′とし、次のような熱機関を考えます。
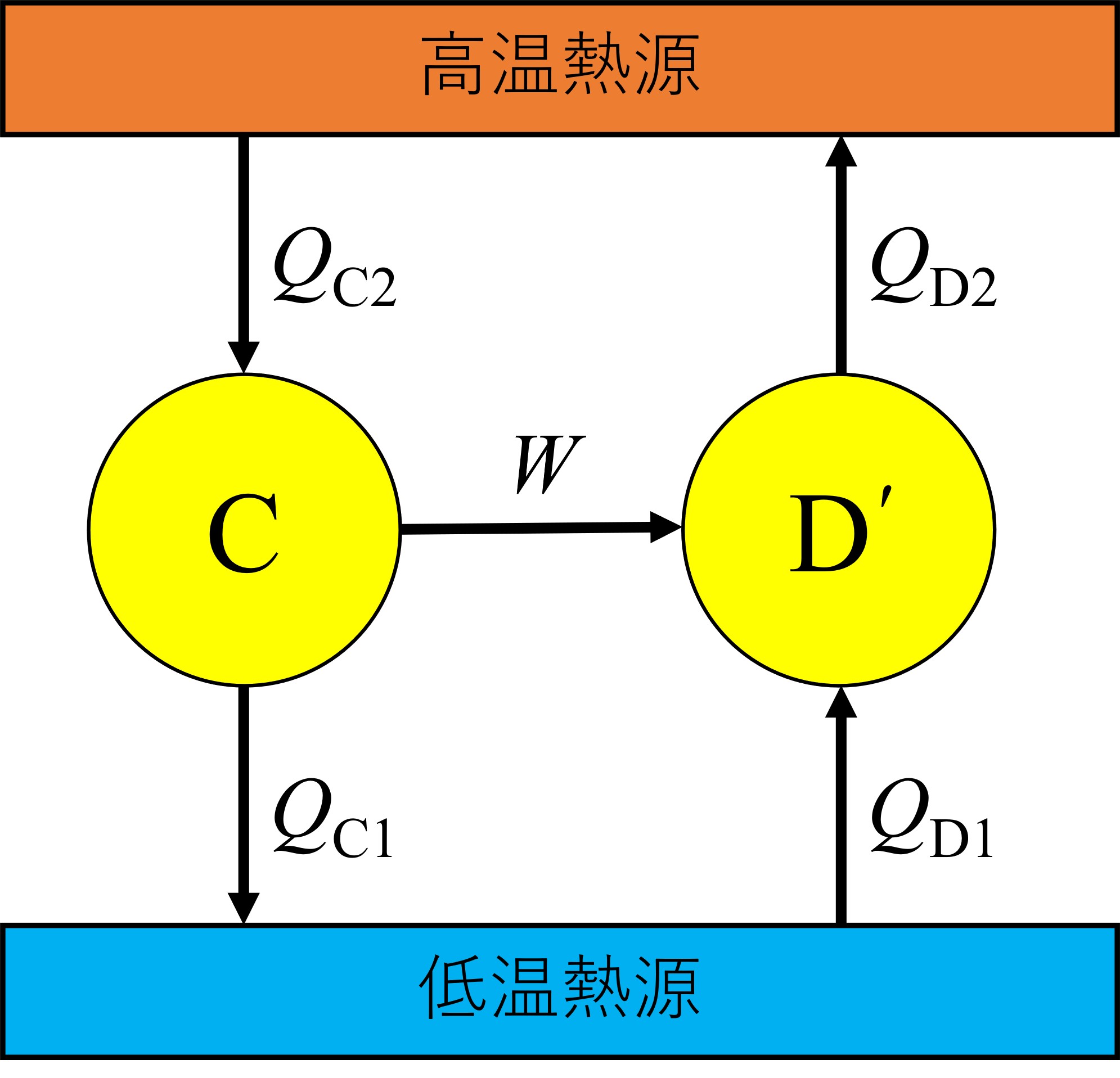
クラウジウスの原理より、
\[
\begin{cases}
Q_\mathrm{C1} \geq Q_\mathrm{D1}\\
Q_\mathrm{C2} \geq Q_\mathrm{D2}
\tag1
\end{cases}
\]
また、図3にある2つのサイクルをどちらも逆サイクルにすると、同様にクラウジウスの原理から、
\[
\begin{cases}
Q_\mathrm{C1} \leq Q_\mathrm{D1}\\Q_\mathrm{C2} \leq Q_\mathrm{D2}
\tag2
\end{cases}
\]
(1)式と(2)式より、
\[
\begin{cases}
Q_\mathrm{C1} = Q_\mathrm{D1}\\
Q_\mathrm{C2} = Q_\mathrm{D2}
\tag3
\end{cases}
\]
よって、Cの熱効率を\(\eta \)、D′の熱効率を\(\eta^\prime \)とすると、
\[
\begin{align}
\eta’ &= 1 – \frac{Q_\mathrm{D2}}{Q_\mathrm{D1}}\\
&= 1 – \frac{Q_\mathrm{C2}}{Q_\mathrm{C1}}\\
&= \eta
\end{align}
\]
ここで重要なのは、理想気体を作業物質としたカルノーサイクルは熱効率が高温熱浴と低温熱浴の温度にのみ依存することです。これはポアソンの法則から導かれるのでした。よって、任意の可逆な熱機関の熱効率は高温熱浴と低温熱浴の温度にのみ依存することがわかります。
今度は、任意の不可逆な熱サイクルEを用いて次のような熱機関を組み立てます。
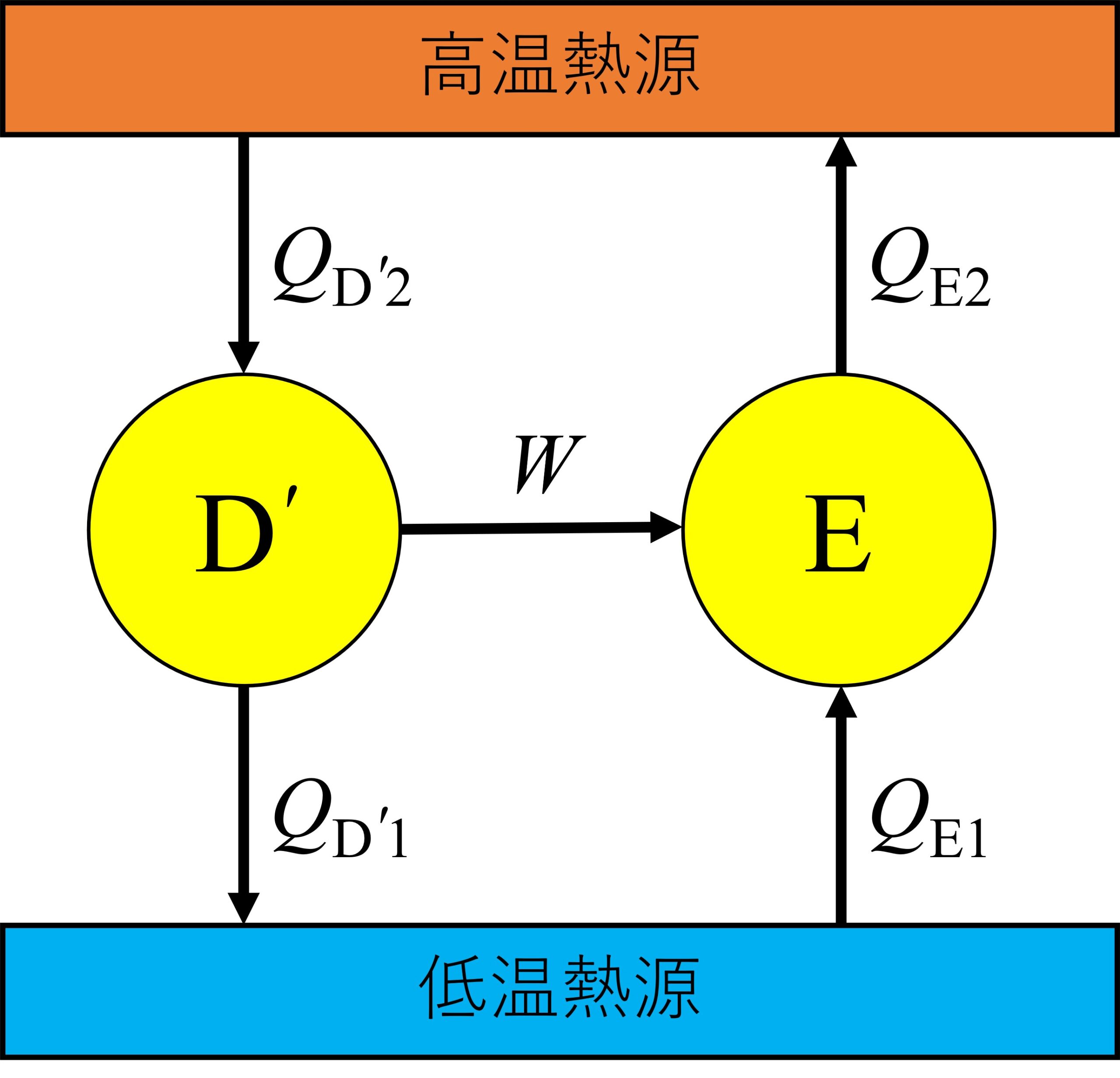
クラウジウスの原理と熱力学第一法則より、
\[
Q_\mathrm{D’2} \geq Q_\mathrm{E2} \tag4
\]
\[
W=Q_\mathrm{E2}-Q_\mathrm{E1}=Q_\mathrm{D^{‘}2}-Q_\mathrm{D^{‘}1}
\tag5
\]
(4)式と(5)式より、Dの熱効率を\(\eta^\prime \)、Eの熱効率を\(\eta^{\prime \prime} \)とすると、
\[
\begin{align}
\eta^{\prime \prime} &= \frac{Q_\mathrm{E2}-Q_\mathrm{E1}}{Q_\mathrm{E2}}\\
&= \frac{Q_\mathrm{D^{‘}2}-Q_\mathrm{D^{‘}1}}{Q_\mathrm{E2}}\\
&< \frac{Q_\mathrm{D^{‘}2}-Q_\mathrm{D^{‘}1}}{Q_\mathrm{D^{‘}2}}
=\eta’
\end{align}
\]
以上で、カルノーの定理が証明できました。
*補足
歴史的には、初めにカルノーの定理が発表され、その後クラウジウスの原理が発表されました。カルノーの定理は熱素説と呼ばれる現在では信じられていない過程を基に考えられていますが、クラウジウスはこれを使わずにカルノーの定理を証明しました。
そしてエントロピーへ
これで熱力学第二法則の説明は以上ですが、最後にエントロピーへの導入をして終わりにします。
高温熱源(温度\(T_\mathrm H\))から熱サイクルに移動した熱を\(Q_\mathrm H > 0\)、低温熱源(温度\(T_\mathrm L\))から熱サイクルに移動した熱を\(Q_\mathrm L < 0\)とします。このとき、カルノーの定理より、
\[
1+\frac{Q_\mathrm{H}}{Q_\mathrm{L}} \leq 1-\frac{T_\mathrm{H}}{T_\mathrm{L}}
\]
\(Q\)を\(T\)で割った値が0か負になるという結果が導かれました。実はこの\(Q/T\)がエントロピー(の原型)になります。化学系の教科書では殆ど説明されていませんが、エントロピーはカルノーの定理から定義された値なのです。
エントロピーについて詳しく知りたい方はこちらをご覧ください。
