ファンデルワールスの状態方程式とは
ファンデルワールスの状態方程式とは、実在気体あるいは液体を記述する方程式です。
\[
\left(
P+a\frac{1}{{\bar{V}}^2}
\right)
(\bar V +b)=RT
\]
実在気体についての概要は、こちらをご覧ください。
【化学向け】理想気体と実在気体の違いについて解説！ | マスケットの大学化学
超臨界流体
通常、気体の圧力を大きくしてゆくと、あるところで液体になりますが、ある温度以上では、圧力の大きさに関わらず気体は液化しないことが知られています。この温度を臨界温度と言い、Tcと表記します。また、臨界温度の時の圧力と体積は一意に定まるることも知られており、それぞれ臨界圧力Pc、臨界体積Vcと言います。また、これらを一般に臨界定数と言います。
ファンデルワールスの状態方程式を用いて、縦軸に圧力、横軸にモル体積をとると次のようなグラフが描けます。
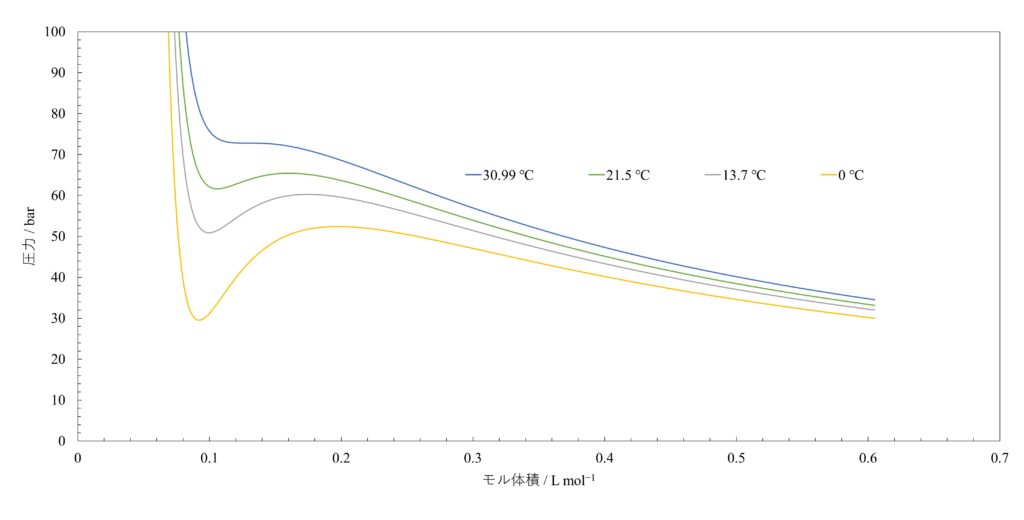
また、山と谷の面積が等しくなるように直線を引き、その直線の上下にある山と谷の線を消すと、実測のグラフとよく一致することが知られています。これをマクスウェルの等面積則といいます。
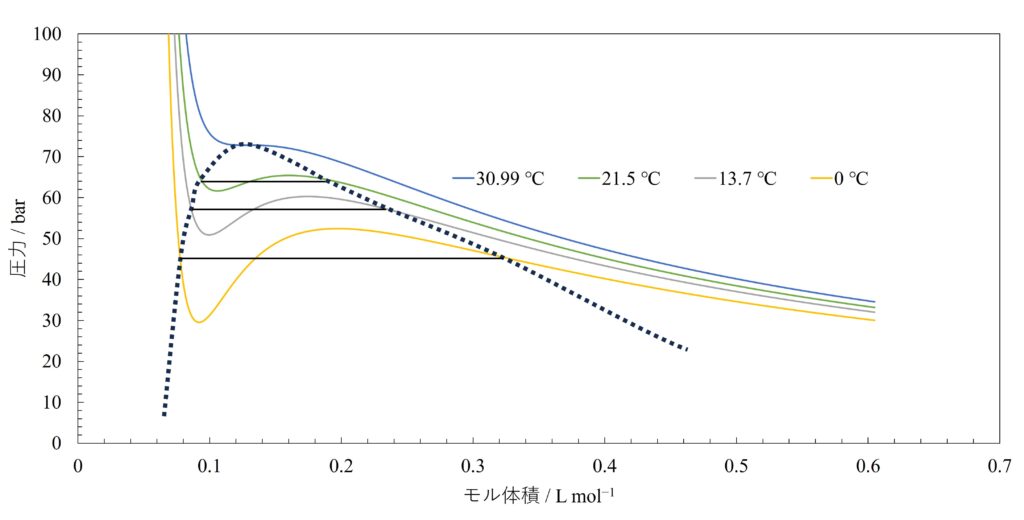
すると、約31 ℃で山と谷がなくなります。これが臨界温度です。また、図2で示した点線の内部は気体と液体が共存する領域です。
対応状態の法則
これから対応状態の法則について説明します。まず、臨界モル体積を\(\bar V\)とすると、ファンデルワールスの状態方程式が\(\bar V\)について3次式であることより、
\[
(\bar{V}-\bar{V}_c)^3=0
\Leftrightarrow
\bar{V}^3-3\bar{V}_c\bar{V}^2+3\bar{V}_c^2\bar{V}-\bar{V}_c^3=0 \tag1
\]
また、ファンデルワールスの状態方程式を展開して、
\[
\left(
P+a\frac{1}{{\bar{V}}^2}
\right)
\left(\bar{V}+b\right)=RT
\]
\[
\bar{V}^3 – \left(b + \frac{RT}{P}\right)\bar{V}^2 + \frac{a}{P}\bar{V} – \frac{ab}{P} = 0
\tag2
\]
(1), (2)より、係数を比較して、
\[
3\bar{V}_c=b+\frac{RT_c}{P_c}
\tag3
\]
\[
3\bar{V}_c^2=\frac{a}{P_c}
\tag4
\]
\[
\bar{V}_c^3=\frac{ab}{P_c}
\tag5
\]
(4)と(5)より、
\[
\bar{V}_c=3b
\tag6
\]
(6)を(5)に代入して、
\[
\begin{align}
(3b)^3 &= \frac{ab}{P_c}\\
P_c &= \frac{a}{27b^2}
\tag7
\end{align}
\]
(6)を(7)と(3)に代入して、
\[
3 \cdot 3b = b + \frac{RT_c}{ \frac{a}{27b^2} } = b + \frac{27b^2RT_c}{a}
\]
\[
\unicode{x2234} T_c = \frac{8a}{27bR}
\tag8
\]
a, bを臨界定数で表してみます。(7)/(8)より、
\[
\frac{P_c}{T_c}=
\frac
{
\frac{a}{27b^2}
}
{
\frac{8a}{27bR}
}
=\frac{R}{8b}
\]
\[
\unicode{x2234} b = \frac{RT_c}{8P_c}
\tag9
\]
(9)を(7)に代入すると、
\[
\begin{align}
a=27b^2P_c &= 27P_c \cdot \frac{R^2 T_c^2}{8^2P_c^2}\\
&=\frac{27R^2T_c^2}{64P_c}
\end{align}
\]
(4)と(5)より、aとbを代入して
\[
a = 3P_c \bar V_c^2\tag{10}
\]
\[
b = \frac{1}{3} \bar{V}_c\tag{11}
\]
これをファンデルワールスの状態方程式に代入して、
\[
\left(
P + \frac{3P_c \bar{V}_c^2}{\bar{V}^2}
\right)
\left(
\bar{V}-\frac{1}{3}\bar{V}_c
\right)
=RT
\]
両辺\(P_c \bar{V}_c\)で割って、
\[
\left(
\frac{P}{P_c} + 3\frac{\bar{V}_c^2 }{\bar{V}^2}
\right)
\left(
\frac{\bar{V}}{\bar{V}_c}- \frac{1}{3}
\right)
=
\frac{RT}{P_c \bar{V}_c}
\tag{12}
\]
ところで、(6), (7), (8)より、
\[
\frac{P_c \bar{V}_c}{RT_c}
=
\frac{
\frac{a}{27b^2} \cdot 3b
}
{
R \cdot \frac{8a}{27bR}
}
=\frac{3}{8}
\tag{13}
\]
これは非常に面白い結果で、左辺の換算定数と気体定数からなる値は気体の種類に依らず3/8、つまり定数になるという事実を主張しています。実際、殆どの気体について臨界定数がこの式をおおよそ満たすことが実験的に知られています。これを対応状態の法則または対応状態の原理と言います。
(13)を(12)に代入して、
\[
\left(
\frac{P}{P_c} + 3\frac{\bar{V}_c^2 }{\bar{V}^2}
\right)
\left(
\frac{\bar{V}}{\bar{V}_c}- \frac{1}{3}
\right)
=
\frac{8}{3} \frac{T}{T_c}
\tag{14}
\]
ここで、換算圧力\(P_R\)、換算モル体積\(\bar{V}_R\)、換算温度\(T_R\)を定義します。
\[
P_R:= \frac{P}{P_c}, \ \bar{V}_R:= \frac{\bar{V}}{\bar{V}_c},\ T_R:= \frac{T}{T_c}
\tag{15}
\]
(15)を(14)に代入して、
\[
\left(
P_R+ \frac{3}{\bar{V}_R^2}
\right)
\left(
\bar{V}_R – \frac{1}{3}
\right)
=
\frac{8}{3} T_R
\]
この形も対応状態の法則の一つとして用いられます。
圧縮因子における対応状態の法則
最後に、圧縮因子も対応状態の法則に従うことを紹介します。
初めに、ファンデルワールスの状態方程式より、
\[
\left(
P+a\frac{1}{{\overline{V}}^2}
\right)
(\bar{V}+b)=RT
\]
\[
P=\frac{RT}{\bar{V}-b} – \frac{a}{\bar{V}^2}
\]
これを用いて圧縮因子を求めると、
\[
\begin{align}
z
&= \frac{P \bar{V}}{RT} \\
&= \frac{\bar{V}}{RT}
\left(
\frac{RT}{\bar{V}-b} – \frac{a}{\bar{V}^2}
\right)\\
&=\frac{\bar{V}}{\bar{V}-b} – \frac{a}{\bar{V}RT} \\
&=\frac{\bar{V}}{\bar{V} – \frac{1}{3} \bar{V}_c} – \frac{3P_c \bar{V}_c^2}{\bar{V}RT}
\tag{(10)より} \\
&= \frac{\bar{V}_R}{\bar{V}_R-\frac{1}{3}} – 3 \cdot \frac{P_c \bar{V}_c}{RT_c\cdot \frac{T}{T_c}} \cdot \frac{\bar{V}_c}{\bar{V}}\\
&= \frac{3\bar{V}_R}{3\bar{V}_R-1} – \frac{9}{8\bar{V}_RT_R}
\end{align}
\]
圧縮因子も換算定数だけで記述することができました。
